|
Elementarmathematische |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
und |
Das didaktische Motto, auf einem Wanderweg bei Weimar gefunden:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Computerprogramme zur handlungsorientierten Entwicklung mathematischer Vorstellungen und Begriffe
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zu allen hier vorgestellten Problemfeldern findet man auch Computerprogramme, die spielerisch handelnd, anschauliche gedankliche Zugänge zu verschiedenen z. T. "klassischen" elementarmathematischen Problemfeldern öffnen können. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Inhalt |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Teiler, arme, reiche, vollkommene und merkwürdige Zahlen |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Spiegelzahlteiler
zum Artikel
(erschienen in: Nolte, M. Was macht Mathematik aus? Nachhaltige paradigmatische Ansätze für die Förderung mathematisch besonders begabter Schüler. Münster: WTM. 2010.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Das Ausgangsproblem In unserem Dezimalsystem hat die Zahl 1089 mehrere bemerkenswerte Eigenschaften. Eine davon ist 1089 · 9 = 9801. Ihre „Spiegelzahl“ ist ein Vielfaches von ihr. Eine kleinere nichttriviale Zahl mit dieser Eigenschaft findet man nur, wenn man führende Nullen zulässt und z. B. an 045 · 12 = 540 denkt. Diese kuriose Eigenschaft der 1089 erscheint – zunächst und isoliert betrachtet – ein belangloser Zufall im Zehnersystem zu sein, der mit der auffälligen Primfaktorzerlegung 1089 = 32 · 112 und einer seltsamen Vielfachenliste (s. unten) wiederum „zufällig“ zusammenfällt.
Die Ziffern der einzelnen Stellenwerte aufeinanderfolgender Vielfacher gehen durch "verdrehen" (= links hoch-, rechts runterzählen) auseinander hervor. Die Liste enthält neben dem trivialen Spiegelzahlteiler 5445 den weiteren nichttrivialen 2178, für den 8712 : 2178 = 4 gilt, der Quotient also Q = 4 ist. Beide Spiegelzahlteiler sind Keimzellen ganzer Serien in denen sich viele weitere auffällige Teilbarkeitsverhältnisse finden, von denen einige wenige hervorgehoben sind:
Man formuliere diese und weitere Aussagen für unser Dezimalsystem allgemein und scharf und beweise oder widerlege sie.
Andere Stellenwertsysteme Eine strukturgleiche Serie findet man in allen Stellenwertsystemen, hier im Sechsersystem:
Hier entstehen also alle Vielfachen des Spiegelzahlteilers 1045 ebenfalls durch verdrehen und sind hier sämtlich selbst wieder Spiegelzahlteiler (das liegt an den vielen Teilern der 6).
Weitere Anregungen zur selbständigen Weiterarbeit findet man im Tagungsband des Festkolloquiums anlässlich des 80. Geburtstags von Prof. Dr. Karl Kiesswetter (erscheint demnächst). Ein zu diesem Beitrag produziertes Computerprogramm kann hier kostenlos heruntergeladen werden. Es erlaubt systematische Suchen nach Spiegelzahlteilern in verschiedenen Stellenwertsystemen.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Graphen-Boss-Puzzle | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Spiel auf Graphen
Der Einsiedlergraph
|
Zum Inhalt:
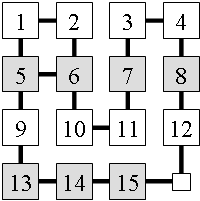
In den frühen 1990er Jahren wurde zu diesem Problemfeld in der Oberstufengruppe des Hamburger Projekts zur Begabtenförderung eine kleine abgeschlossene Theorie erarbeitet. Bei dem üblichen 15er-Spiel bemerkt man schnell, dass es zwei Äquivalenzklassen von Belegungen gibt. Es ist zum Beispiel nicht möglich, die 1 mit der 2 zu vertauschen und alle anderen Zahlen stehen zu lassen. (s. auch W.Ahrens: Mathematische Unterhaltungen und Spiele, Leipzig 1918) Wenn man das Spiel von der üblichen Schiebemechanik befreit (wie links im Bild angedeutet, dort sind auch schon einige Zugmöglichkeiten weggelassen), kann man es auf beliebigen Graphen spielen und sich die Frage vorlegen, wie viele Äquivalenzklassen von Belegungen es abhängig vom Spielgraphen gibt. Für den unten abgebildeten Spielgraph sind dies z. B. 6 Klassen. Man kann beweisen, dass es, bis auf triviale Sonderfälle (Kreise und nur einfach zusammenhängende Graphen), bei denen es beliebig viele Klassen geben kann, nur Graphen mit 1, 2 oder 6 Äquivalenzklassen gibt. Bei der Analyse dieses Spieles kommt man um das Spielen natürlich nicht herum. Dazu wird ein Computerprogramm bereitgestellt, mit dessen Editor man beliebige Spielgraphen erzeugen und auf ihnen spielen kann. Bei diesem Spielen werden wichtige Beobachtungen gemacht und man bemerkt, wie diese Beschäftigung zur selbstverständlichen Verknüpfung immer längerer Handlungsketten zu neuen Denkeinheiten, wir nennen sie „Superzeichen“, führt. Durch sie werden dann auch komplexere Situationen beherrschbar und die Entwicklung einer Theorie maßgeblich erleichtert.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sudoku | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ratefelder mit Hervorhebungen
Kleinsche Vierergruppe, Mini-Sudoku
Regimenteraufgabe, Leonhard Euler von Katharina der Großen gestellt |
Zum Inhalt:
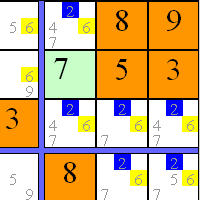
Sudoku-Rätsel sind mathematisch äußerst interessant. Sie bieten von der Grundschule bis zur Universität viele Möglichkeiten zur experimentellen theoriebildenden mathematischen Arbeit. Es gibt z.B. Bezüge zur Kombinatorik (der Kunst des Zählens) und zur Algebra. Im Handbuch werden verschiedene Problemfelder zur mathematischen Beschäftigung vorgestellt. Als Herausforderung für den Leser enthält es auch zahlreiche Aufgaben und Hinweise auf ungelöste Probleme. Das Computerprogramm wurde zur Förderung der Kreativität von mathematisch begabten Schülern und Studenten entwickelt und ist sehr breit angelegt. Man kann Rätsel bearbeiten, erzeugen, analysieren, verändern, mit verschiedenen Algorithmen lösen lassen, etc. Damit ist es für den Spieler ebenso geeignet wie für den mathematisch Interessierten. Das Programm kann in der Schule zum individualisierten problemorientierten Unterricht eingesetzt werden. Für den an algebraischen Strukturen Interessierten besteht z. B. auch die Möglichkeit zu untersuchen, welche fertig ausgefüllten Sudokus als das Innere einer Gruppentafel hinsichtlich der verschiedenen in Frage kommenden Gruppen deutbar sind. Man kann z. B. zeigen, dass jedes 4x4-Sudoku eine Gruppentafel der Restklassengruppe modulo 4 oder der Kleinschen Vierergruppe ist oder danach fragen, welche fertig ausgefüllten 9x9-Sudokus Gruppentafeln der Z9 oder der Z3xZ3 sind. Interessant ist auch ein Zusammenhang zur Geschichte der Mathematik. Es wird berichtet, dass Leonhard Euler in St. Petersburg von Katharina der Großen die folgende Aufgabe gestellt wurde: Aus 6 Regimentern werden jeweils 6 Offiziere mit unterschiedlichem Rang gewählt. Ist es möglich, diese 36 Offiziere in einem 6x6-Karree so aufzustellen, dass in jeder Reihe bzw. in jeder Spalte jeder Rang genau einmal vorkommt und je ein Offizier aus jedem Regiment? Für 6 Regimenter gibt es keine solche Aufstellung, aber für vier Regimenter wird eine solche Aufstellung durch die Überlagerung zweier Mini-Sudokus erreicht. Die Farben im Bild links stehen für die Regimenter, die Kopfbedeckungsform für die Ränge. Wie man sieht, sind beide Merkmale in der Art eines gelösten Mini-Sudokus verteilt. Die Lösung leistet damit noch mehr, als Katharina sich wünscht: Auch in jedem 2x2-Unterquadrat, das ein Eckquadrat des 4x4-Quadrats enthält, kommt jeder Rang und jedes Regiment vor. Sudoku, Materialien zum entdeckenden Lernen, eine Handreichung |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Efron-Würfel-Ringe | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nicht transitive "besser-als-Relation"
Efrons paradoxes Würfelset
Äquivalenzklasse von Würfelringen
Beweisfigur für lim(p) = 3/4 |
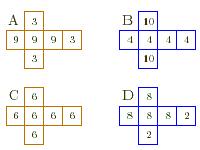
Zum Inhalt: Zwei Spieler verabreden mit den „kuriosen Würfeln“ von Bradley Efron folgendes Spiel: Spieler X wählt einen Würfel und wirft eine Zahl. Dann wählt Y einen anderen Würfel und wirft ebenfalls. Wer die höhere Zahl wirft, gewinnt. "Kurios" scheint, dass Y bei diesem Spiel im Vorteil ist, seine Gewinnchance beträgt genau 2/3, also ca. 66%, obwohl X doch die erste Wahl hat und sich somit den besten Würfel nehmen könnte! Die "besser-als-Relation" ist hier - gegen alle sprachgewohnheitsbedingte Erwartung - nicht transitiv, sie bildet einen Ring. Im Hamburger Projekt zur Begabtenförderung haben wir dieses spezielle Würfelset zum Ausgangspunkt für weitergehende Fragestellungen genommen. Drei Leitfragen zu einer kleinen Theorie nichttransitiver Würfelringe:
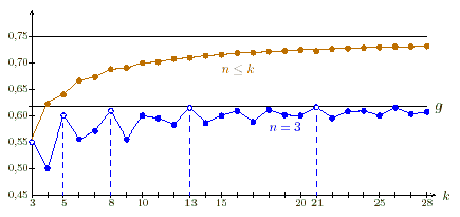
Bei der Analyse z. T. durch die Programmierung eines Computers gewonnener Daten findet man auffällige Muster. Die Tabelle zeigt die mit n k-seitigen Würfeln höchste realisierbare Gewinnwahrscheinlichkeit an der schwächsten Stelle eines Efron-Würfel-Rings.
Auffällig ist die streng monotone Konvergenz an 3/4 (wenn man so viele k-seitige Würfel verwenden darf, wie man will) und die herausragende Rolle der Fibonaccizahlen, wenn man nur 3 Würfel verwenden darf.
Bei der Analyse wird eine neuartige graphische Repräsentation solcher Ringe verwendet, die unendlich viele konkrete Sets zu Äquivalenzklassen zusammenfasst und die zyklische Struktur der Efron-Ringe widerspiegelt. Damit eignet sie sich für visuell veranlagte Menschen hervorragend zur Gewinnung und zum Beweis einiger Einsichten über solche Würfelringe. Ausarbeitung eines Vortrags zur Herbsttagung 2006 der Mathematischen Gesellschaft Hamburg: Mitteilungen der mathematischen Gesellschaft Hamburg, Band 26. Hamburg 2007, S. 27-42 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Das Lampenproblem | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Kann man jedes Leuchtmuster herstellen?
Laras Aufgabe
Schaltvektoren über GF(2) |
Eine Anzahl Lampen ist mit einer Anzahl E/A-Schalter vernetzt. Jeder Schalterdruck wechselt den Lampenzustand jeder mit dem Schalter verbundenen Lampe. Welche Leuchtmuster kann man durch welche Schaltsequenzen herstellen? Mit dem Computerprogramm kann man solche funktionsfähigen Schaltwerke am Bildschirm editieren. Das Spielprogramm stellt zu der jeweils aktuellen Schaltung Fragen und Aufgaben und bewertet die Reaktionen des Spielers.
Rückmeldefenster des Programms Die Idee zu diesem Programm stammt aus einem vor einigen Jahren sehr beliebten Abenteuer-Spiel, bei dem die virtuelle Akteurin Lara zwar hauptsächlich herumrennen und -schießen musste, aber manchmal eben auch Rätsel lösen sollte, um einen Level weiterzukommen. Lara sollte bei einer bestimmten Schaltung 7 Lampen anknipsen. Bei jeder Lampe stand ein Schalter, dieser wirkte aber vertrackterweise auch auf die beiden Nachbarlampen. Schaltete man nun also 6 Lampen an, was leicht war, so führte die Betätigung des Schalters bei der siebten Lampe leider dazu, dass zwei Nachbarlampen wieder ausgingen... Die Arbeit in diesem Problemfeld kann durch einen Repräsentationswechsel in n-dimensionale Vektorräume über dem endlichen Körper mit zwei Elementen führen. Man kann wahlweise auch in dieser Repräsentation mit Matrizen arbeiten. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ziegenproblem und Eulers e-Funktion | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Aus dem Computerprogramm
|
Die wahrscheinlichkeitstheoretische Analyse des sogenannten Ziegenproblems ist eigentlich sehr einfach. Dass es dennoch eine z. T. sogar hitzig geführte öffentliche Diskussion auslöste, liegt sicher auch in den paradox erscheinenden Widersprüchen zwischen verschiedenen Sichtweisen und dem "naiven Gefühl" für Wahrscheinlichkeiten. Im graphisch animierten Simulationsprogramm kann man den Kandidaten spielen (in Form einer bekannten Persönlichkeit aus Entenhausen) und verschiedene Spielstrategien auf ihre Erfolgsträchtigkeit hin testen. Die Zahl der Türen kann erhöht werden. Die Möglichkeit, ganze 20er Spielblöcke im Zeitraffer abzulaufen zu lassen (man definiert dabei sein Entscheidungsverhalten im vorhinein, s. links, mittleres Bild), macht das Programm zu einem bequem zu verwendenden "Monte-Carlo-Hypothesen-Tester". Bei der Analyse des verallgemeinerten Spiels zeigen sich überraschende Strukturen. So führt z. B. die Strategie "wähle jedesmal eine neue Tür, nachdem der Moderator eine Tür mit Ziege geöffnet hat", auf eine Gewinnwahrscheinlichkeit, die eng mit der Reihenentwicklung der Exponentialfunktion verknüpft ist.
Strebt die Zahl der Türen gegen unendlich und man wählt jedesmal nach dem Wegfall einer Tür eine der verbleibenden, so strebt die Gewinnwahrscheinlichkeit gegen 1 - 1/e. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Der Turm von Hanoi auf vier Unterlagen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Eine besondere Zwischenstellung
Teilansicht Programmoberfläche |
Bei diesem Spiel, sollen n verschieden große Scheiben, die zunächst der Größe nach sortiert auf einer von vier Unterlagen liegen, auf eine andere Unterlage transportiert werden. Dabei darf immer nur eine Scheibe umgelegt werden und zwar nur auf eine leere Unterlage oder auf eine größere Scheibe. Für drei Unterlagen ist dieses Spiel sehr einfach zu analysieren und man erwartet zunächst keine besonderen Schwierigkeiten bei vier Unterlagen. Umso überraschender ist es, dass es bis heute niemandem gelungen zu sein scheint zu beweisen, dass die in der Tabelle angegebene Folge V(n) die Minimalzahl der Umlegeprozesse für die gewünschte Turmwanderung angibt (D(n) gibt diese Anzahl für drei Unterlagen an).
Dass der Anfang der angegebenen Folge V(n) eine obere Schranke für die gesuchte Minimalzahl ist, kann konstruktiv dadurch gezeigt werden, dass man Umlegeprozesse mit einer besonders gearteten teilsortierten Zwischenstellung, bei der die größte Scheibe bewegt werden kann, angibt (die Tabelle wird dann iterativ aufgebaut). Leider ist (nach meinen Recherchen) bis heute noch niemandem ein Beweis dafür gelungen, dass man für das gesuchte Minimum von einer solchen teilsortierten Zwischenstellung ausgehen darf. Mit Hilfe des Programms kann man per Hand oder mit Monte-Carlo-Algorithmen bequem eigene Untersuchungen vornehmen. Man kann - als Makro-Operation - auch ganze Teiltürme im Stück bewegen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Halbierbare Sequenzen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Teilansicht aus dem Programm "Sequenzierer" |
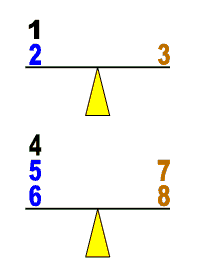
1 + 2 = 3 ist eine interessante Rechnung.
1 + 2 + 3 + 4 + 5 + ... + 14 = 15 + 16 + 17 + 18 + 19 +20 sieht ähnlich aus. 4 + 5 + 6 = 7 + 8 schließt an 1 + 2 = 3 nahtlos an. 9 + 10 + 11 + 12 = 13 + 14 + 15 schließt wiederum nahtlos an 4 + 5 + 6 = 7 + 8 an! Geht das wohl so weiter? Schließt sich auch an die zweite Gleichung nahtlos eine weitere an? Wie ist überhaupt das gesamte Spektrum solcher Gleichheiten strukturiert? Die Suche nach Ausschnitten aus der Folge der natürlichen Zahlen, die sich in zwei summengleiche Abschnitte zerlegen lassen, führt zur Entdeckung ästhetisch äußerst reizvoller "Interpunktionsmöglichkeiten" bei den natürlichen Zahlen. Tiefere Struktureinsichten und Beweise führen z. T. in die Zahlentheorie, lassen sich aber oft auch mit figurierten Zahlmustern erfassen und begründen:
In diesem Bild liegt ein Schlüssel zu einer Erkenntnis Eine Anschlussfrage führt in den Bereich verallgemeinerten Fibonaccizahlen und zu einem Problem mit Quadratzahlen in arithmetischen Progressionen, das von Leonhard Euler gelöst wurde. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Irrfahrten | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zweidimensionales Histogramm
am Rand gelandet |
Sehr viele Zufallsprozesse sind als Irrfahrt auf einem Graphen deutbar. Bei großzügiger Auslegung kann man das ganze Leben als Irrfahrt auf einem (unendlichen) Zustandsgraphen mit leider genau einem absorbierenden Zustand auslegen. Das Programm dient zur statistischen Untersuchung symmetrischer und nichtsymmetrischer Irrfahrten auf ein- zwei- und dreidimensionalen Gittern. Man sieht ein bekanntes kleines rotes Auto über ein frei skalierbares Gitter huschen. Besuchshäufigkeiten markanter Orte (Heimatkreis oder Ränder) werden angezeigt.
Die resultierende "Brownsche Molekularbewegung" wird dadurch, dass der Wagen Spuren hinterlässt, die mit jeder Streckenbefahrung breiter werden, als zweidimensionales Histogramm angezeigt. Es gibt viele Einstellmöglichkeiten. download des Computerprogramms |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Zufallsgeneratoren | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zufallszahlenmuster?
Definition des ZG im Programm
Folge für sehr kleine Parameter |
Zufallszahlen werden häufig gebraucht. Sei es für elektronische Glücksspiele, wahrscheinlichkeitstheoretische Untersuchungen mit der Monte-Carlo-Methode oder zufallsgesteuerte Musikauswahl in elektrischen Geräten oder Computerprogrammen usw. Die mathematische Modellierung des Zufalls wird häufig mit sogenannten Kongruenzgeneratoren vorgenommen. Diese erzeugen natürlich alles andere als "wirkliche Zufallszahlen", denn sie arbeiten deterministisch iterativ mit der Gleichung x(n+1) = a*x(n) +b modulo M. Diese Generatoren erzeugen Perioden, die bestenfalls die Länge M haben. Es gibt zwar hilfreiche zahlentheoretische und algebraische Einsichten, aber die Auswahl guter Parameter ist auch heute noch ein experimentelles Feld der Mathematik. Man kann diese Generatoren im Programm definieren und analysieren. Z. B. arbeitet der TI-59 mit a = 24298, b = 99991 und M = 199017 und hat eine maximale Periodenlänge. Das Programm unterstützt eine visuelle Qualitätsprüfung solcher Generatoren. Die Zufallszahlen werden als Punkte im dreidimensionalen Raum gedeutet. Man kann Raumsektoren definieren und die Projektionen der Zufallspunkte in die Ebene ansehen. Dabei werden auch subtile Muster sichtbar. Das links im Bild zu sehende Streifenmuster findet man auch bei den besten Zufallsgeneratoren und ist prinzipiell nicht vermeidbar (Satz von Marsaglia, 1968).
Sprungverhalten für sehr kleine Parameter |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Zur Fibonaccifolge modulo n | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zyklenlängen modulo n
Phyllotaxis 5/8 · 2pi
Aus dem Programm FiPhy (Fibonacci-Phyllotaxis-Analysator)
|
1. Problemfeld, die Zyklenlänge der Fibonaccifolge modulo n Ein einfacher Schubfachschluss beweist, dass die Fibonaccifolge modulo n für jedes n zyklisch ist und dass die Zyklenlänge Z(n) kleiner als n2 ist. Eine mit Hilfe eines kleinen Computerprogramms gewonnene Tabelle bis n = 199 zeigt ein recht sprunghaftes Verhalten der Funktion Z(n) und vor allem auch, dass die Zyklenlänge in der Regel deutlich unter n2 bleibt. Das stimmt nachdenklich. Eine Materialsammlung zur Mustererkennung führt schnell zu verschiedenen Hypothesen und zu der Erkenntnis, dass es, wie so oft bei zahlentheoretischen Fragen, reicht, hinsichtlich der Primzahlpotenzen pa Klarheit zu schaffen. Die Betrachtung von Z(pa ) zeigt dann auch schnell auffällige arithmetische Muster, die zu hypothetischen Sätzen führen. Eine im 20sten Jahrhundert formulierte (recht zentrale) Hypothese harrt meines Wissens bis heute nach einem Beweis. Die Breite des Themas lässt es sehr wahrscheinlich erscheinen, dass eine Vielzahl interessanter elementarmathematischer Fragen bis heute vielleicht noch nicht einmal gestellt wurde und man daher mit etwas Glück und Hartnäckigkeit nicht nur subjektiv Neues verschiedener Tiefe finden und beweisen kann (in einer Bachelorarbeit in diesem Themenbereich gab es solche Ansätze).
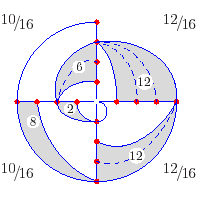
2. Problemfeld, Modellierung guter Raumnutzung durch optimale Phyllotaxis Angeregt durch die Feststellung, dass die Phyllotaxis der Sonnenblume der Goldene Winkel sei - also 360°/F, ungefähr 222,5°, das entspricht 137,5° in der Gegenrichtung kann man auf die Idee kommen, den folgenden zyklischen Auffüllprozess zu betrachten: Man ordnet eine gewisse Anzahl n von freien Plätzen zyklisch an und füllt diese dann – stets um dieselbe Schrittzahl k in eine Richtung weitergehend – zyklisch auf (man lässt dort ein Blatt oder einen Kern wachsen). Das Bild zeigt diesen Auffüllprozess für n = 8 und k = 5, das jeweils neu hinzugekommene Blatt ist etwas heller dargestellt. Bei dem links dargestellten Prozess ist die Phyllotaxis also 135° (bzw. 225° gegen den Uhrzeigersinn) und somit wird der Goldene Winkel schon ganz gut approximiert. Welche biologischen Vorteile bzw. mathematischen Besonderheiten damit verbunden sein könnten, ist an diesem kleinen Zahlenbeispiel noch nicht zu sehen. Insbesondere bleibt es noch begrifflich unscharf, was eine gute Raumnutzung bedeuten könnte, bzw. wie man diese mathematisch modellieren kann Verschiedene Modelle werden vorgestellt und ein Computerprogramm zur visuellen und arithmetischen Darstellung lädt zur eigenen Weiterforschung ein.
Deutschsprachiges Manuskript zu The length of cycles in Fibonacci-sequences modulo M In: Fritzlar, T., Problem Solvin in Mathematics Education, Proceedings of the ProMath conference 2007, August 30 - September 2 in Lüneburg. Franzbecker, Hildesheim, Berlin 2008. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Quadratische Irrationalitäten | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Approximation von Wurzel 5
Kettenbruch "normal" und gespiegelt |
Visualisierungen durch das Programm Approximation Das Bild links zeigt einen Ausschnitt der Bildausgabe des Programms "Approximation". Zu sehen ist, wie gut eine Approximation der Wurzel aus 5, mit Brüchen deren Nenner zwischen 9 und 17 liegt, gelingt. Der Bruch 29/13 verbessert den Bruch 20/9 und dann ist erst wieder eine Verbesserung mit dem Nenner 17 erreichbar. Alle diese Näherungsbrüche sind kleiner als die gesuchte Wurzel. Diese graphische Darstellung wird für beliebige quadratische Irrationalitäten bis zum Nenner 10201 gezeigt. Man sieht geheimnisvolle zyklische graphische Muster mit leichten Störungen ihrer "Wellenlänge". Darüber hinaus werden in einem Textfenster weitere interessante Angaben gemacht. Das Programm kann dazu dienen, die Qualität rationaler Näherungen, die durch verschiedene algorithmische Verfahren, wie etwa Kettenbrüche, iterative Lösungsfolgen Pellscher Gleichungen, Heron-Verfahren usw. gewonnen wurden zu untersuchen und miteinander zu vergleichen. Es ist faszinierend zu sehen, wie einige Algorithmen mit geradezu "traumwandlerischer Sicherheit" von einer herausragenden Näherung über viele Nenner hinweg zu einer weiter rechts liegenden herausragenden Näherung springen. Dabei entdeckt man bei den Algorithmen auffällige Unterschiede in der Sprungweite. Kettenbruchentwicklung nach Perron und gespiegelt Das Programm erzeugt für beliebige quadratische Irrationalitäten die Kettenbruchentwicklung und gibt diese wahlweise in der Bruchschreibweise oder in der von Oskar Perron verwendeten Klammerschreibweise aus. Als weiteren Untersuchungsgegenstand kann man sich eine "gespiegelte" Variante dieser normalen Kettenbruchentwicklung anschauen und bei diesen ebenso Fragen zur Struktur und Konvergenzgeschwindigkeit oder Ähnliches bearbeiten.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abdrift, Kurse bei Strömung | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 Knoten Strömung aus Süd Autopilot ein
Weitere Einstellmöglichkeit und Datenausgabe
Vorbeigetrieben, die Strömung war zu stark
Radiodrome:
Steuerung nach Leitstrahl oder auf Sicht, stets genau auf das Ziel zu.
Bei einer Strömung (Luft oder Wasser) wird das Fahrzeug (Flugzeug oder
Schiff) abgetrieben und der Kurs muss (im theoretischen Grenzfall)
ständig angeglichen werden. |
Welchen Weg nimmt ein Schiff, wenn der Steuermann trotz Strömung stets stur auf die Insel zuhält? Welchen Kurs sollte man abhängig von Strömung und eigener Fahrt durchs Wasser nehmen, um das Ziel möglichst schnell zu erreichen? In welchem Verhältnis steht die Fahrtstrecke über Grund zur Fahrt durchs Wasser? Welche Ziele kann man erreichen, wenn die Fahrt des Schiffes langsamer ist als die Strömung? Mit dem Computerprogramm Abdrift können diese und weitere Fragen experimentell untersucht werden. Man bedient den Steuerstand eines Schiffes. Das Steuerrad wird von einem Zeiger auf einer Windrose gebildet. Die Seekarte zeigt ein Planquadrat des blauen Meeres von 100x100 Seemeilen und die frei wählbare Strömungsrichtung und -stärke. Die Zielinsel und das Schiff sind frei positionierbar.
Das Programm modelliert die Situation auf See mit Differenzengleichungen. Neben der geometrischen Veranschaulichung erhält man realistische Daten zur weiteren Auswertung. Sollte man mit Differentialgleichungen arbeiten, kann das Programm zur experimentellen Überprüfung der Ergebnisse verwendet werden. Radiodromen, Homing und Differentialgleichungen Artikel "Kurse bei Strömung" pdf Die ersten Zeilen: Ein Schiff halte bei konstanter Meeresströmung stets genau auf das Ziel zu. Das heißt, dass so gesteuert wird, dass der Bug des Schiffes mit Hilfe eines sichtbaren Ziels (z. B. eines Leuchtturms) oder mit Hilfe eines Peilstrahls, stets auf das Ziel ausgerichtet ist. Das Schiff fährt dann eine sogenannte Radiodrome, was Leitstrahlkurve heißt. Ohne Strömung würde es sich also auf einer Geraden bewegen, die direkt zum Ziel führt. Mit Strömung entsteht i. A. eine gekrümmte Kurve, denn das Schiff wird durch die Strömung versetzt, der Kurs muss also ständig korrigiert werden. In einer analogen Situation befindet sich ein Flugzeug im Wind. Der Zielanflug nach dieser Strategie wird dort als „Homing“ bezeichnet. Wenn die Fahrt des Schiffes durchs Wasser schneller ist als die Meeresströmung, kann man zu jedem Ziel gelangen, sonst nicht. In dem Artikel wird eine Differentialgleichung und ihre Lösung für dieses Problem vorgestellt. Die Kurve ist mit der sogenannten "Hundekurve" (Hund läuft Herrchen hinterher) verwandt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Diophantische Dreiecke | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
aus 8 Streichhölzern kann man nur ein Dreieck legen
Beispiel Programmausgaben |
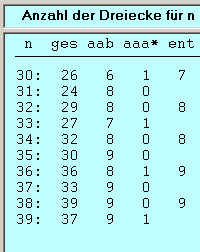
In dem Band Aufgaben und Lehrsätze aus der Analysis I von Pólya/Szegö (1925)* findet man die Frage nach der Anzahl der Lösungen der diophantischen Gleichung s1 + s2 + s3 = n, die der Nebenbedingung s1 + s2 ≤ s3 und s2 + s3 ≤ s1 und s3 + s1 ≤ s2 genügen (alle Variablen sollen aus IN sein). Die Nebenbedingung ist die Dreiecksungleichung und es liegt daher nahe, die Aufgabe geometrisch zu interpretieren. Gefragt ist nach der Anzahl von Dreiecken, die sich aus einer gegebenen Anzahl Streichhölzer legen lässt. Im Folgenden zählen wir die nicht entarteten Dreiecke. (D. h. wir setzen in die Nebenbedingungen ein "echt kleiner". Für die Frage nach der Anzahl der Lösungen ist das weder eine Vereinfachung noch eine Erschwernis, hat man das eine Problem gelöst, so fällt die Lösung des anderen jeweils leicht). Ganz offensichtlich sind es weniger, als es Zerlegungen der Zahl n in drei Summanden gibt, da die Summanden zusätzlich die Dreiecksungleichung erfüllen müssen. Nimmt man Streichhölzer als Einheiten, so stellt man schnell fest, dass man aus 8 Hölzern nur genau ein Dreieck legen kann (durch Seitentausch ergeben sich noch zwei zu diesem kongruente Dreiecke, wir zählen also Äquivalenzklassen). Der Anfang der Folge A(n) zeigt - als Hinweis darauf, dass dieses Zählproblem nicht ganz einfach ist - ein ziemlich sprunghaftes Verhalten.
Da diese Aufgabe gerade als Seminaraufgabe verwendet wird, werden keine Bearbeitungstips gegeben, sondern nur ein Computerprogramm bereitgestellt, mit dessen Hilfe man seine Hypothesen überprüfen kann. Das Programm zählt - je nach Wunsch - die entarteten Dreiecke mit oder nicht.
*Pólya, G./Szegö, G.(1925). Aufgaben und Lehrsätze aus der Analysis I. Grundlehren der mathema-tischen Wissenschaften, Band 19, Berlin.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Räuber-Beute-Simulation | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bestandsverlauf
Phasendiagramm
|
Der Verlauf der Bestandsgrößen nach dem Modell von Volterra wird in verschiedenen Repräsentationen dynamisch dargestellt. Die Parameter können verändert und die Wirkung analysiert werden. Man sieht eine Unterwasserlandschaft, Räuber- und Beutefische und kann in die laufende Simulation eingreifen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Flucht der Panzerknacker | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Dieses Programm bezieht sich auf die Aufgabe E1 aus Kapitel 4 in MatheNetz 8 aus dem Westermann Verlag. Die Panzerknackerbande hat die Bank von Entenhausen überfallen und ist auf der Flucht. Die gelben Strecken markieren von der Polizei aufgestellte Lichtschranken. Gefragt ist nach der Wahrscheinlichkeit bei „kopfloser Flucht“ zu entkommen. Durch viele Einstellmöglichkeiten (man kann Lichtschranken ein- und ausschalten, das hin- und herlaufen erlauben oder verbieten), reicht der "mathematische Gehalt" der Simulation von der Mittelstufe (Baumdiagramme) bis zur Oberstufe (Markoffketten). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Das Frankierungsproblem (auch als Münzproblem bekannt) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
N = x·5 + y·8
27 geht nicht 28 = 4·5 + 1·8 29 = 1·5 + 3·8 30 = 6·5 31 = 3·5 + 2·8 32 = 4·8 ...
59 = -17·5 + 18·8 59 = -9·5 + 13·8 59 = -1·5 + 8·8 59 = 7·5 + 3·8 durch das Aufsteigen bei x und das Absteigen bei y in den positiven Bereich gekommen
N = x·5 + y·11 + z·13
19 geht nicht 20 = 4·5 21 = 2·5 + 1·11 22 = 2·11 23 = 2·5 + 1·13 24 = 1·11 + 1·13 25 = 5·5 26 = 2·13 27 = 1·5 + 2·11 28 = 3·5 + 1·13 29 = 1·5 + 1·11 + 1·13 usw.
N = x·6 + y·10 + z·15 Ab S = 30 ist alles darstellbar
Die 31 geht so: 31= 1·6 + 1·10 + 1·15
Grafik zur arithm. Progression mit den Markenwerten 7, 12, 17
|
Ein bekanntes Problem der elementaren Zahlentheorie lautet:
Welche Portobeträge N kann man mit nur zwei Markenwerten A, B bezahlen? Die Markenwerte A, B seien natürliche Zahlen und so lautet die Frage: Welche natürlichen Zahlen N lassen sich in der Form N = xA + yB mit natürlichen Zahlen (inklusive 0) x, y darstellen? Durch die Schreibweise N = (x, y)·(A, B) := xA + yB wird eine geometrische Sicht der Dinge betont. Im Folgenden soll der Fall ggT(A, B) = 1 betrachtet werden, denn es lassen sich natürlich nur Vielfache des ggT darstellen und die Frage, ab welcher Grenze S (und ob überhaupt) jedes Vielfache vom ggT darstellbar ist, kann durch das Herausdividieren des ggT stets auf den teilerfremden Fall zurückgeführt werden. Unmittelbar klar ist auch, dass dann, wenn man auch negative x und y zulässt jede natürliche Zahl N in der Form N = (x, y)·(A, B) darstellbar ist (wegen der Darstellbarkeit der 1, deren Darstellung man z. B. leicht mit Hilfe des Euklidischen Algorithmus findet). Satz 1 Für zwei natürliche teilerfremde Zahlen A und B ist ab und inklusive der Grenze S = (A – 1)·(B – 1) jede natürliche Zahl N in der Form N = (x, y)·(A, B) mit natürlichen Zahlen x, y darstellbar.
Anmerkung: Man kann das auch so ausdrücken: Die größte nicht darstellbare Zahl ist N=AB-A-B.
Man nennt diese Zahl die Frobeniuszahl und diesen Satz den "Satz von
Sylvester". Hier wird mehr als Satz 1 behauptet (nämlich auch Satz 2,
weiter unten) Eine einfache Beweisidee wird durch eine graphische Deutung geliefert, die schon durch die Benennung der Parameter mit x und y nahegelegt wird. Jeder Gitterpunkt (ganzzahlig) des Koordinatensystems repräsentiert eine Zahldarstellung. Für das Beispiel A = 5 und B = 8 repräsentieren alle Punkte, die man um (-8, 5) oder (8, -5) verschiebt dasselbe N (wegen 0 = (–8)·5 + 5·8 ), es gibt also Äquivalenzklassen. Die Lösungen der Ungleichung N = xA + yB ≥ (A-1)(B-1), hier also 5x + 8y ≥ 24 werden durch alle Rasterpunkte oberhalb der fallenden blau-roten Geraden in der Abbildung links repräsentiert. Die Forderung, dass x und y nichtnegativ sind heißt nun, dass man sich für Gitterpunkte im ersten Quadranten (inklusive der Achsen) interessiert. Man zeigt nun, dass es für jedes N ≥ (A-1)(B-1) einen Repräsentanten (x, y) im ersten Quadranten gibt: Anmerkung: In der geometrischen Deutung heißt das, dass auf jeder Geraden
ein (ganzzahliger) Gitterpunkt des ersten Quadranten liegt. Die Abbildung links skizziert diese Aussage für (A, B) = (5, 8). Im Beweis springt man von Gitterpunkten mit x < 0 zum nächsten rechts von x liegenden Gitterpunkt auf der Geraden so oft weiter, bis man im weißen Bereich landet. Dass diese Grenze scharf ist, lässt sich leicht zeigen: Satz 2 N = AB - A - B ist nicht in der Form N = xA + yB (alles natürliche Zahlen) darstellbar. Beweis: AB - A - B = xA + yB ergibt umgeformt die Forderung AB = (x+1)A + (y+1)B, die wegen der Teilerfremdheit von A und B mit nichtnegativem x und y nicht erfüllbar ist.■ Weitere bekannte Ergebnisse (bis zur Grenzzahl ab der jedes Porto darstellbar ist, ist genau die Hälfte aller Beträge darstellbar und Anderes) können ebenfalls in der geometrischen Repräsentation besonders anschaulich bewiesen werden. Eine Verallgemeinerung auf drei Marken ist interessant
Zur Untersuchung wird ein
Computerprogramm bereitgestellt, das es gestattet, die Zahldarstellungen für
frei wählbare drei Markenwerte anzuschauen. Es soll dabei helfen, Muster und
Hypothesen zu finden bzw. auf ihre Richtigkeit hin abzuklopfen. Das Programm
zeigt an, welche N man nur mit einem Markenwert darstellen kann (die drei oberen
Zeilen), welche N mit je zwei Markenwerten darstellen kann (die drei mittleren
Zeilen) und welche N man darstellen kann, wenn man alle drei Markenwerte A, B, C
verwendet. Dazu eine Anregung (ein bekannter Spezialfall, an dem man sich eigenständig versuchen kann):
Die Markenwerte A = 6, B = 10 und C
= 15 sind paarweise nicht teilerfremd, aber der größte
gemeinsame Teiler aller drei Zahlen ist 1.Die Frobeniuszahl ist 29 und
diese kann auf eine bestimmte Art aus a = 2, b = 3 und c = 5 berechnet werden. Diese drei Zahlen sind paarweise teilerfremd und A, B, C sind die drei Zahlen, die durch paarweise Multiplikation von a, b, c entstehen. Man probiere also verschiedene Möglichkeiten, hebe eine Hypothese ab und beweise diese.
Bildausschnitt aus der Programmoberfläche
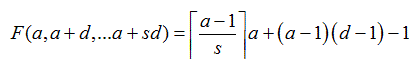 Die Grafik zur arithmetischen Progression links visualisiert die (einfache) Beweisidee: Man sortiert nach der Anzahl der geklebten Briefmarken, denn diese Anzahl bestimmt den Rest der dargestellten Zahl modulo d. Man überlegt sich dann, ab welcher Stelle man die Zahlen zu den Resten modulo d lückenlos darstellen kann. Der Beweis kann hier heruntergeladen werden. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fordkreise | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
zoomen:
↓klick↓
↓groß↓
Einstellungen:
|
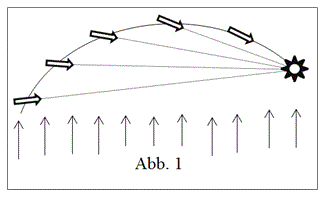
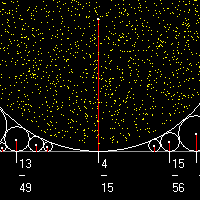
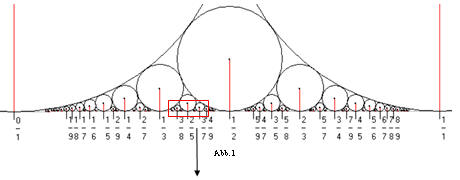
Die rationalen Zahlen nehmen ein Schaumbad. Dabei liegt auf jeder rationalen Zahl auf der x-Achse der reellen Ebene genau eine ebene „Seifenblase“, also ein Kreis. Auf der rationalen Zahl mit der ausgekürzten Darstellung q = r/s liegt auf dem Zahlenstrahl ein Kreis mit dem Durchmesser 1/s2 . In jedem noch so kleinen Intervall liegen unendlich viele ausgekürzte Brüche (da die rationalen Zahlen dicht liegen) und zwischen je zwei dieser Brüche liegen dann wiederum unendlich viele und so ad infinitum weiter. Möchte man nun auf jede rationale Stelle einen Kreis stellen (mit Radius > 0), so sagt einem die Anschauung wohl ein ziemliches "Gedrängel" vorher und man möchte meinen, dass so ein Unterfangen nicht ohne Überschneidungen möglich ist. Abbildung 1 zeigt die Situation für das Intervall [0, 1] für alle Brüche deren Nenner höchstens 13 ist.
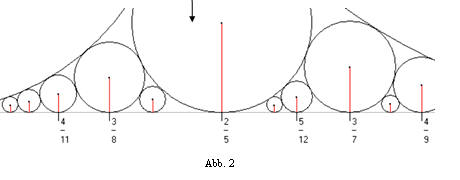
Auf 0 und 1 liegen Kreise mit dem Durchmesser 1, bei ½ liegt ein Kreis mit dem Durchmesser ¼. Nun sieht es so aus, als fänden alle diese Kreise überschneidungsfrei nebeneinander Platz. Einige Kreise berühren einander. Abbildung 2 zeigt eine Ausschnittsvergrößerung.
1938 entdeckte der amerikanische Mathematiker Lester Ford diese Kreise und ihre ganz erstaunlichen Eigenschaften, wie Überschneidungsfreiheit (obwohl doch auf jeder rationalen Zahl ein Kreis liegt und die rationalen Zahlen dicht liegen!), Bedingungen für direkte Berührung, gemeinsame Berührung zweier berührender Kreise an einen dritten Kreis, etc.
Mit dem Computerprogramm KreiZ, (Freeware) kann man "Erkundungsfahrten" in die Welt der Fordkreise unternehmen und selbständig nach geometrischen und arithmetischen Mustern und ihren Beziehungen forschen. Dabei entdeckt man z. B. schnell, dass die "falsche Addition" von Brüchen "Zähler plus Zähler und Nenner plus Nenner (die Farey-Addition) hier einen ganz besonderen geometrischen Sinn hat.. Gemäß des oben wiedergegebenen Goethe-Zitats sollte man aber auch hier erst einmal "anschauen". Dabei wird man von dem Programm durch Zoom-, Scroll- und Markierungsfunktionen auf nützliche Weise unterstützt. In der Bildleiste links ist z. B. eine 100-fache Vergrößerung des Ausschnitts um den Kreis bei 4/15 zu sehen. Man kann bis zum 10.000fachen vergrößern und den Ausschnitt im Intervall [0, 1} beliebig laufen lassen (die Bewegung ist animiert). Man kann wählen, bis zu welchem Nenner man sich die Kreise und ihre Berührstellen auf dem Zahlenstrahl anzeigen lässt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Teiler
Arme, reiche, vollkommene, merkwürdige und andere Zahlen. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
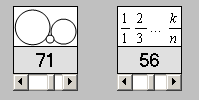
Skyline auf dem Zahlenstrahl: Teiler der Zahlen 55 bis 60
auffällige Primfaktorzerlegung der geselligen Zahl 12496 aus dem Fünferzyklus 12496 - 14288 - 15472 - 14536 - 14264
|
Hier kann ein kleines graphisch orientiertes Computerprogramm zur Darstellung der Funktionswerte zweier zahlentheoretischer Funktionen (Teileranzahl t(n) und Summe der echten Teiler s*(n)) heruntergeladen werden. Eine Suchfunktion hilft beim Aufspüren von Zahlen mit speziellen Funktionswerten s*(n) = an + b. Die Wahl (a, b) = (0, 1) filtert z.B. die Primzahlen, die Wahl (a, b) = (1, 0) die vollkommenen Zahlen und (a, b) = (2, 0) die doppelt vollkommenen Zahlen heraus. Man kann durch die freie Wahl von a und b aber auch Zahlen mit ganz anderen speziellen Eigenschaften suchen und Hypothesen für eigene mathematische Sätze bilden. Ganz interessant ist es z.B., abundante Zahlen (s*(n) > n) zu betrachten mit s*(n) = n + v, wobei v eine vollkommene Zahl ist. Durch die im Programm integrierte Funktion zur Primfaktorzerlegung hat man ein Werkzeug zur Hypothesenbildung zur Hand.
Ausschnitt aus dem Collatz-Graph der Nachfolgerbildung "Summe der echten Teiler von". Stabile Kreissysteme und im "schwarzen Loch" endende Reisen . 70 ist reich und kann dennoch nicht als Summe einiger ihrer Teiler geschrieben werden, man sagt, 70 sei eine merkwürdige Zahl |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Aus dem Computerprogramm Statische Kolonien und Krabbler
Definition von 2^16 Welten
Definition der Von-Neumann-Nachbarschaft
Im Programm abrufbare Beispiele
Einstellmöglichkeiten Mit Hilfe des Programms kann man •zelluläre Automaten definieren (Überführungsregeln festlegen), •Anfangsmuster frei zeichnen, •den Verlauf beobachten, •im Verlauf vor- und zurückgehen, •in den Verlauf eingreifen und die Wirkungen beobachten, •während des Ablaufens die Überlebensbedingungen (die Überführungsregeln) ändern und schauen, welche Strukturen aussterben oder zum Leben erwachen, •Farben und Rastergröße einstellen (man kann die Zellen - je nachdem, wie lange sie schon leben - farblich unterscheiden, •Welten laden und speichern •die Darstellung mehrerer Takte überspringen (das ist nützlich, wenn man die Frequenz zyklischer Verläufe untersuchen will). und sich über die unauslotbar vielen Überraschungen freuen, denn es gibt 2^16 Welten, also mehr als 65000 2^10000 Startkonstellationen auf einem 100x100 Raster, das sind ungefähr 20000000000000000000000...000 (mehr als dreitausend Nullen) das ist deutlich mehr, als die Schätzung der Anzahl der Elementarteilchen im Universum. Es ist also völlig unmöglich, alles auszuprobieren und man kann hier noch echte Neuentdeckungen machen. |
Wir betrachten ein Muster aus ausgefüllten Quadraten und
leeren Quadraten auf Karopapier.
●Die ausgefüllten Quadrate nennen wir lebende Zellen, die anderen unbelebte Zellen, es gibt also genau zwei Zellzustände. Nun legen wir eine einfache Entwicklungsregel fest: ►Hat eine lebende Zelle genau 2 oder 3 lebende Nachbarn, so lebt sie auch noch in der nächsten Generation, sonst nicht. ►Hat eine unbelebte Zelle genau 3 Nachbarn, so erwacht sie in der nächsten Generation zum Leben, sonst nicht. Es ist klar, dass man auch andere Überführungsregeln aufstellen kann (s. Spalte links). Die Folgen der genannten Festlegung untersuchte der Mathematiker Conway in den 1970er Jahren (das Spiel wurde ursprünglich von Ulam im Jahre 1940 erfunden). Die folgende Bildsequenz zeigt eine Entwicklungsfolge:
Man sieht Ausgangslage in blau, die ersten 3 Folgegenerationen und die 16 Generation. Ab der 18. Generation gerät die Entwicklung in einen stabilen Zweierzyklus. In rot sind neu zum Leben erwachte Zellen dargestellt, in schwarz solche, die schon in der vorhergehenden Generation lebten.
Beispiele: 2345_3 "Korallenwachstum" Nahezu jeder kleine Zellhaufen wächst sehr langsam zu einer labyrinthischen Struktur heran. Dabei lagern sich neue Zellen außen an, die Bestandteil des dauerhaften Gerüsts werden. Verblüffenderweise wächst nicht der ganze Rand. Ohne, dass sich dem Auge ein Unterschied erschließt, kommt es immer wieder zu inaktiven Randbereichen, die durch einwandernde Randaktivitäten wieder belebt werden. So entstehen ausgesprochen überraschende mit Aus- und Einbuchtungen versehene Objekte.
568_34568 "Hirn" erzeugt aus Zufallsmustern verschwindende oder pulsierende bei Verletzung (Löschen vorhandener oder Einbringen neuer Zellen) selbstheilende Strukturen. Nahezu jede zur Zeit k lebende Zelle stirbt und wird neu belebt in einem Zweierzyklus (blinkende Struktur). Andere (also länger lebende Zellen) gibt es fast nicht. Diese "wachsen" allerdings als Tumore, falls bei der Überlebensbedingung die 7 dazugenommen wird und heilen nach Entfernen der 7 wieder aus.
23_3 Conways Welt wimmelt von seltsamen Objekten. Man findet krabbelnde Zellhaufen, Strukturen, die an Windmühlen erinnern und sich zu drehen scheinen, auskristallisierte starre Objekte, Gleiterkanonen und vieles mehr. Es ist auch hier faszinierend, sich zurückzulehnen und dynamische Verläufe zu beobachten.
4567_4568 "Baukasten" erlaubt den Bau von Strukturen, die wie Förderbänder aussehen (Beispiel zum Ausprobieren muss die Datei heruntergeladen werden und vom Programm ZellAu aus geöffnet werden). Eingebrachte kleine kompakte Zufallsobjekte sterben oder schrumpfen zu lebensfähigen 2-Phasen Blinkern. Große löcherige Zufallsobjekte zerfallen und die Komponenten sterben zumeist.
Seit dem 9. Juni 2014 Verbesserte Version: Installationsprogramm für ZellAu2.2 zip (Freeware) Im ZIP-Ordner zum Herunterladen (entpacken und setup.exe ausführen) Wer nicht installieren möchte, sondern mit der reinen exe-Datei arbeiten will, findet diese im Ordner Support zip. Dort stehen auch die ggf. benötigten Steuerelemente und Programmbibliotheken zum freihändigen Nachinstallieren (das erfordert Kenntnisse) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Impressum Angaben gem. § 5 TMG Betreiber und Kontakt Dr. Hartmut Rehlich, Bienroder Weg 87 38106 Braunschweig Alle Bilder und Graphiken sind eigene Bilder |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Link zur Institutsseite: |
Dr. Hartmut Rehlich, IDM TU Braunschweig, Bienroder Weg 97, 38106 Braunschweig | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Disclaimer
Eine Bitte: Sollten dem Leser dieser Seiten Fehler in Orthographie, Sinn und Verstand auffallen, so bittet der Verfasser um Nachsicht und Nachricht und bittet auch darum, die Tücken der Technik (auf die auch andere hingewiesen haben) zur Entschuldigung ins Kalkül zu ziehen:
|
O unberachenbere Schreibmischane, Du tappst die falschen Tisten, luber Bieb! von J. Guggenmoos |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Alle Programme dürfen heruntergeladen, beliebig genutzt und weitergegeben werden. Die meisten Programme werden nach dem Herunterladen in ein selbst zu wählendes Verzeichnis einfach als exe-Datei durch Doppelklick gestartet. Für einige Programme (Sudoku, Efron-Würfel-Ringe und Boss-Puzzle) können Installationsprogramme heruntergeladen werden. Zu diesen Programmen werden dadurch auch einige Anwendungsdateien (z. B. vordefinierte Spiele) im Programmverzeichnis abgelegt. Es werden keine Einträge in die win-ini-Datei oder irgendwelche anderen Systemdateien gemacht. Nach dem Deinstallieren ist also wirklich alles wieder weg (bei den reinen exe-Dateien ist das sowieso der Fall). Sudoku ist das einzige Programm, das als Shareware angeboten wird, alle anderen sind in vollem Funktionsumfang gratis. Die etwas eingeschränkte Version von Sudoku darf aber auch gratis und beliebig lange verwendet, kopiert usw. werden. Bei Interesse an einer Vollversion kann man 9,99€ auf ein Konto überweisen, und eine Email an mich schicken (beides wird im Programm erklärt). In der Regel sollte alles reibungslos funktionieren, es sei denn, Microsoft nimmt im Laufe der ständigen Aktualisierungen Änderungen an zentralen Systemfunktionen vor, die ich beim Programmieren noch nicht vorhersehen konnte. Mindestens von Windows 95 bis 2010 läuft alles. Wenn etwas nicht geht, wird es aber keinen Unfug stiften, sondern lediglich nicht funktionieren. Aber natürlich installieren und verwenden Sie alles aus freiem Entschluss und jegliche Haftung meinerseits ist ausgeschlossen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||