|
Der Turm von Hanoi auf vier Unterlagen eine Abschätzung, eine offene Frage und ein Spielprogramm aktualisiert im November 2018 |
|
|
Im Hamburger Projekt zur Begabtenförderung haben wir uns mit dem bekannten Spiel "der Turm von Hanoi" beschäftigt. Bei dem Ausgangsspiel auf drei Unterlagen kommt man schnell zu leicht beweisbaren Erkenntnissen. |
|
|
Zur Spielregel:
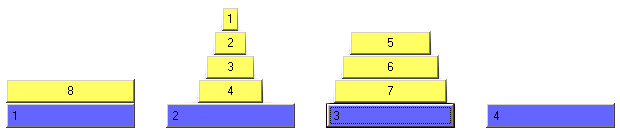
Der Turm auf Unterlage 1 soll auf Unterlage 3 transportiert werden. Dabei darf stets nur die obere Scheibe eines beliebigen Teilturms bewegt werden. Man darf diese auf eine leere Unterlage oder auf eine Unterlage mit einer größeren Scheibe legen (Abb.1). Abb. 1 |
|
|
Zum "Eindenken" kann man die drei folgenden Aufgaben bearbeiten: 1. Man zeige, dass ein solcher Umlegeprozess stets möglich ist. 2. Wie viele Züge werden mindestens benötigt. 3. Wie oft werden die einzelnen Scheiben bei einem solchen Umlegeprozess mindestens bewegt. |
|
|
Diese Aufgaben sind nicht schwierig. Ist man einmal auf die Idee gekommen, den Prozess rekursiv oder iterativ ab- bzw. aufzubauen, so findet man heraus: Der Turm mit n Scheiben kann genau dann transportiert werden, wenn man den Turm mit n-1 Scheiben transportieren kann. Man sieht das sofort ein, wenn man sich klar macht, dass die folgende Zwischenstellung notwendigerweise eingenommen werden muss (Abb. 2).
Abb. 2: Zwischenstellung; die größte Scheibe wird umgelegt Um den Turm mit 6 Scheiben zu bewegen, muss vorher der Turm mit 5 Scheiben bewegt werden und dieser kann nur geordnet auf genau einer Unterlage stehen, denn dann muss die größte Scheibe bewegt werden und daraufhin muss der Turm mit 5 Scheiben noch einmal bewegt werden. Die Anzahl der mindestens nötigen Umlegungen für 6 Scheiben auf drei Unterlagen D(6) ist also D(6) = 2·D(5) + 1. Man sieht sofort, dass dies die Folge der um 1 verminderten Zweierpotenzen erzeugt und beweist dann D(n) = 2n -1 mit Hilfe vollständiger Induktion . So weit so gut. |
|
|
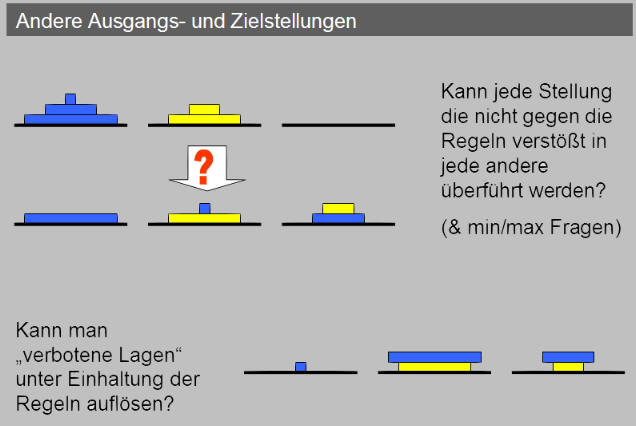
Es gibt für drei Unterlagen weitere interessante Anschlussfragen
z.B.:
|
|
|
Zur (nach unseren damaligen Recherchen)
damals offenen Frage. Inzwischen (das war im Jahre 2014) hat Thierry Bousch vom Laboratoire de Mathematique der Universität Paris nachgewiesen, dass die im Folgenden beschriebene Rekursion tatsächlich die Minimalzahlen liefert. zum Artikel |
|
|
Herleitung der Rekursionsformel Wie groß ist die minimale Zugzahl V(n), wenn man eine vierte Unterlage hinzunimmt? Der Schlüssel zur Analyse bei drei Unterlagen liegt darin, dass man sich überlegt, wie die Situation, bei der man die größte Scheibe bewegt, aussehen muss. Wir versuchen diesen Schlüssel wieder zu verwenden und stoßen auf ein Problem. Auch hier muss es wieder eine Zwischenstellung geben, bei der die größte Scheibe bewegt werden kann. Diese Zwischenstellung muss so aussehen, dass alle Scheiben - bis auf die größte - auf genau zwei Unterlagen verteilt sind. Leider lässt sich aus dieser Situation keine einfache Rekursionsgleichung herleiten (Abb. 3).
Abb. 3: Zwischenstellung; die größte Scheibe wird umgelegt
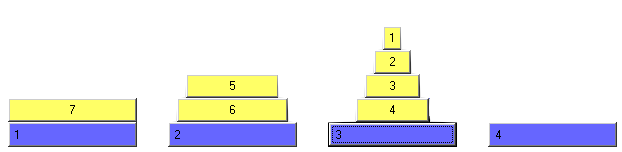
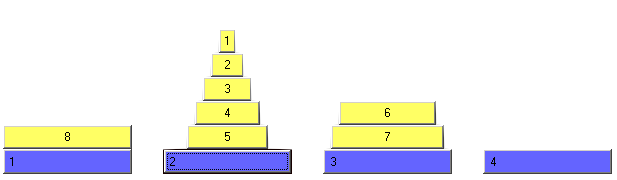
Wir nehmen nun zusätzlich an, dass die Zwischenstellung eines optimalen Umlegeprozesse stets so geartet sein kann, dass eine gewisse Anzahl Scheiben von der kleinsten bis zu einer größeren in lückenloser natürlicher Reihenfolge auf einer Unterlage liegt und der Rest (der auch leer sein kann) auf einer anderen Unterlage liegt. Wenn es auch optimale Prozesse mit gleicher Zugzahl anderer Struktur gibt, stört das ja nicht (Abb. 4 zeigt eine derartige "wohlgeordnete" Zwischenposition).
Abb. 4: Zwischenstellung; die größte Scheibe wird umgelegt, die Scheiben der Teiltürme sind lückenlos zusammenhängend
►Die große Scheibe liegt frei (damit sie bewegt werden kann). ►Auf einer der Unterlagen liegen die m nächstkleineren m Scheiben (in Folge). ►Auf einer der Unterlagen liegen die restlichen k Scheiben. Das Spezielle an dieser Zwischenstellung ist also, dass die beiden Teiltürme übereinander gestellt den Turm aus n-1 Scheiben ergeben. Natürlich gibt es auch dann, wenn man annimmt, dass die Zwischenstellung von dieser Struktur sein darf (um mit der kleinstmöglichen Anzahl von Umlegeprozessen auszukommen) einige Möglichkeiten für die Aufteilung des Turmes aus n-1 Scheiben. Wir nehmen also an, dass unter den minimalen Umlegeprozessen (es kann ja mehrere Wege mit Minimalzahl geben) stets auch wenigstens einen mit einer derart sortierten Zwischenstellung gibt. Jedenfalls lässt sich nun feststellen,
So ergibt sich für V(n) die Rekursion V(n) = min{2·V(k) + 2·D(m)| k + m = n-1} + 1
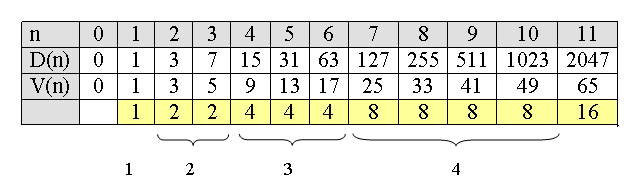
und damit iterativ die folgende Tabelle
Beispiel: Wir nehmen an, wir hätten die Tabelle erst bis n=7 fertig und wollen nun aus den vorhandenen Tabelleneinträgen bis n=7 also V(8) berechnen. Durch systematisches Probieren findet man, dass V(8) auf zwei Arten realisiert werden kann:
V(8) = 2V(4) + 2D(3) + 1 = 18 + 14 +1 = 33 mit dieser Zwischenstellung, oder
V(8) = 2V(5) + 2D(2) + 1 = 26 + 6 +1 = 32 mit dieser Zwischenstellung.
Man entnimmt der Tabelle für n<8, dass man für alle anderen Zwischenstellungen auf eine höhere Zugzahl kommt. Die letzte Zeile der Tabelle zeigt die Differenzenfolge von V(n) mit einer sehr einfachen Struktur und es ist auch nicht allzu schwierig, eine explizite Formel zu entwickeln. |
|
|
Seit 2014 ist klar, dass man davon ausgehen darf, dass sich die minimale Anzahl nötiger Scheibenbewegungen immer durch einen Umlegeprozess realisieren lässt, bei dem die Zwischenstellung nur aus lückenlosen Teiltürmen besteht. |
|
|
Für
mehr als 4 Unterlagen ist die Frage, ob man von sortierten
Zwischenstellungen ausgehen darf (bei 5 Unterlagen wären bei der
Bewegung der größten Scheibe also die restlichen Scheiben
auf drei Unterlagen verteilt) übrigens bis heute offen. (Recherche
im November 2018) Die folgenden Berechnungen und Beweise sind dagegen relativ einfach:
1. Beweis, dass V(n) die Differenzenfolge 1, 2, 2, 4, 4, 4, 8, 8, 8, 8, 16... hat (die k-te Zweierpotenz kommt k+1-mal vor, in der kanonischen Reihenfolge) 2. Berechnung einer expliziten Formel für V(n) 3. Bestimmung der Folgen für mehr als 4 Unterlagen unter einer gewissen rekursiven Annahme (deren Berechtigung bis heute ungeklärt ist). zu 1: Beweis durch vollständige Induktion. Die Idee für den Induktionsschritt wird an einem musterhaften Beispiel erläutert. Bis n = 10 liege die Differenzenfolge vor. Die Summe der ersten 10 Differenzen ist V(11). Zur Berechnung von V(12) wird ein passendes k und m gesucht. 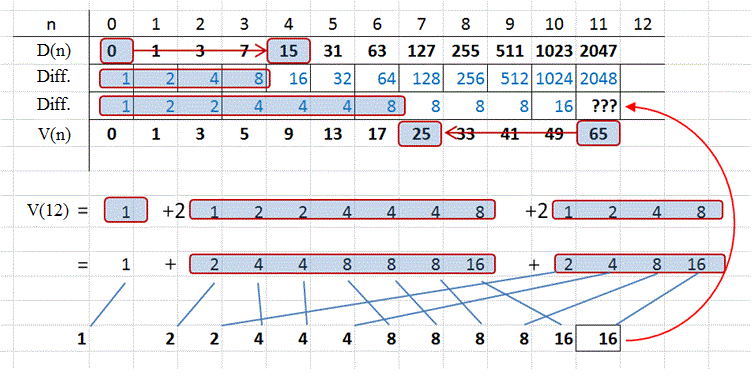 Wie man sieht, liegt das daran, dass ab hier bei D(m) mehr hinzukommt, als man bei V(k) verliert. Hieraus
ergibt sich - ganz allgemein - dass man von der Differenzenfolge von
V(n) so viele Glieder streicht, wie der Exponent der letzten Differenz
(als Zweierpotenz aufgefasst) angibt und diese mit 2 multipliziert und
zusammenzählt und dazu noch ebensoviele Glieder der Differenzenfolge
von D(n) mit 2 multipliziert und dazuzählt und zum Schluß 1
addiert. So verlängert sich die Differenzenfolge in der behaupteten
Weise.
Hier ist noch einmal ein "Beweis ohne Worte" zu sehen: 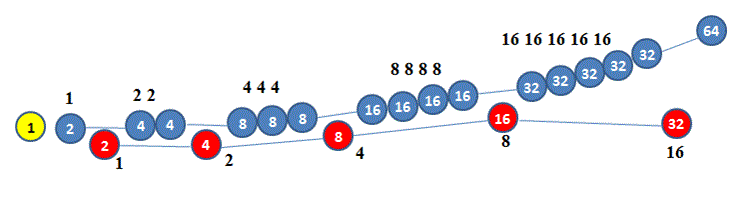 zu 2:  zu 3: Hier findet man durch systematisches Probieren die folgenden Folgenanfänge: 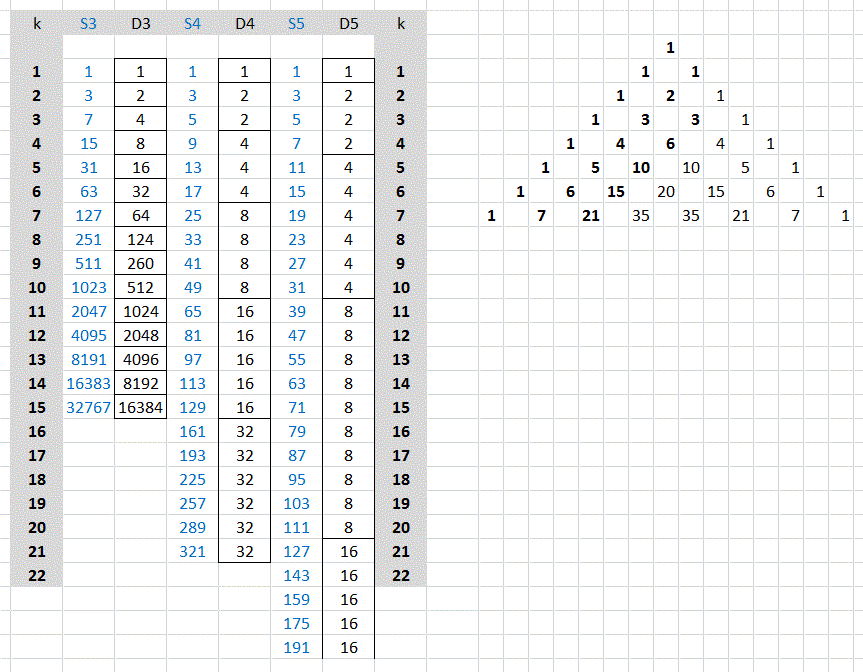 Die Differenzenfolgen dieser Wertefolgen bestehen sämtlich aus Zweierpotenzen in der Vielfachheit von Pascalzahlen. Man kann auch hier - analog zu dem oben Gezeigten - wieder leicht beweisen, dass die Rekursion Wertefolgen mit genau diesen Differenzenfolgen erzeugt. Die analogen Rekursionen für mehr Unterlagen erfordern, dass man über alle wohlgeordneten Zwischenpositionen (während die größte Scheibe wandert) das Minimum betrachtet. Man kann ersatzweise mit einer Rekursion arbeiten, die nur auf den "unmittelbaren Vorgänger der Wertefolgen", also auf die Werte für eine Unterlage weniger zruückgreift und auf kleinere Werte der aktuell untersuchten Wertefolge, wenn man annimmt, dass die Turmspitze auf eine Unterlage transportiert wird und da solange unbehelligt bleibt, bis der Sockel zu seinem Zielfeld gewandert ist. |
|
|
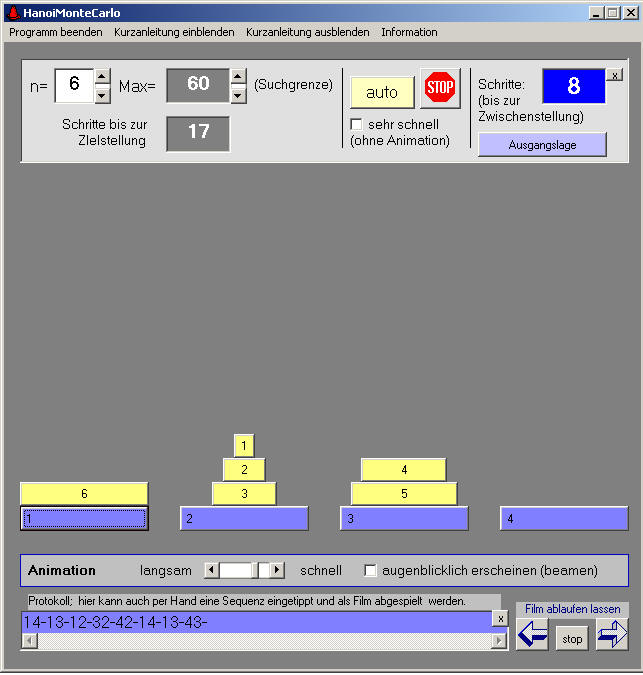
Hier wird ein Computerprogramm zum Spielen und Analysieren angeboten. Man kann 'per Hand' spielen oder einen Monte-Carlo-Suchalgorithmus bei der Arbeit beobachten. Als "Superoperationen" können auch ganze Teiltürme im Stück bewegt werden. Zur Ästhetik: Die Scheiben sind animiert und bewegen sich - ganz im Sinne der newtonschen Mechanik - auf Wurfparabeln. |
|
|
die Programmoberfläche |
|
|
download des Programms (64KB, Freeware) |
|