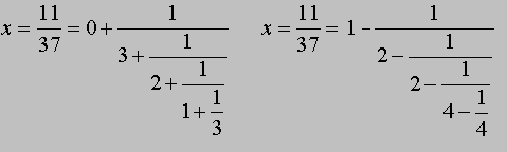
Zur Approximation quadratischer Irrationalitäten
1. Kettenbrüche - normaler und "komplementärer" Algorithmus
Der normale Algorithmus zur Kettenbruchentwicklung funktioniert bekanntlich so:
a) Man spaltet von der positiven darzustellenden Zahl x den ganzen Anteil [x] (Gaußklammern) ab. Es ist dann x = [x] + y.
b) Falls y = 0 ist, ist man fertig. Sonst ist y < 1 und somit der Kehrwert 1/y > 1. 1/y übernimmt nun die Rolle von x und man fährt wie unter a) fort.
Als komplementären Algorithmus bezeichne ich eine Variante, bei der man nicht die nächstkleinere ganze Zahl herauszieht, sondern die nächstgrößere:
a) Man spaltet von Zahl x, falls diese nicht ganz ist, die nächstgrößere Ganzzahl [x+1] (Gaußklammern) ab. Es ist dann x = [x] - y.
b) Falls y = 0 ist, ist man fertig. Sonst ist y < 1 und somit der Kehrwert 1/y > 1. 1/y übernimmt nun die Rolle von x und man fährt wie unter a) fort.
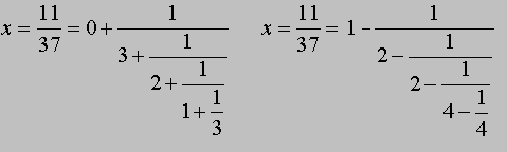
Beispiel 1: Für rationale Zahlen brechen beide Verfahren ab.
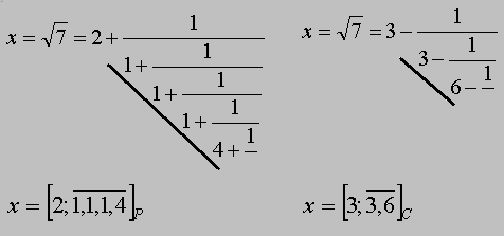
Beispiel 2: Entwicklung der Wurzel aus 7 nach O. Perron und komplementär.
Beide Verfahren liefern periodische Darstellungen.
Mit dem Programm "QuaKEn" (Kettenbruchentwicklung quadratischer Irrationalitäten) kann man für beliebige quadratische Irrationalitäten beide Kettenbruchentwicklungen darstellen. Die Ausgabe erfolgt wahlweise in Bruchdarstellung ("graphisch") und in der von Oskar Perron verwendeten Klammerschreibweise.
Darüberhinaus wird in einem Fenster die Folge der ersten 20 approximierenden Brüche und in einem anderen Fenster die Folge der Koeffizienten der Folge der x (im oben angegebenen Algorithmus) angezeigt.
Damit ist das Programm ein kräftiges Werkzeug zur Analyse und zum Vergleich der beiden Entwicklungen, die ja beide eine approximierende Folge rationaler Zahlen liefern.
Man kann zunächst fragen, welche mathematischen Sätze zu der "normalen Kettenbruchentwicklung" auch für die komplementäre Entwicklung gelten. Darüberhinaus kann man z. B. auch Vergleiche anstellen:
1. Welche Folge konvergiert für welche Vorgaben schneller?
2. Können die Folgen gemeinsame Glieder haben?
3. Welche Symmetrien findet man?
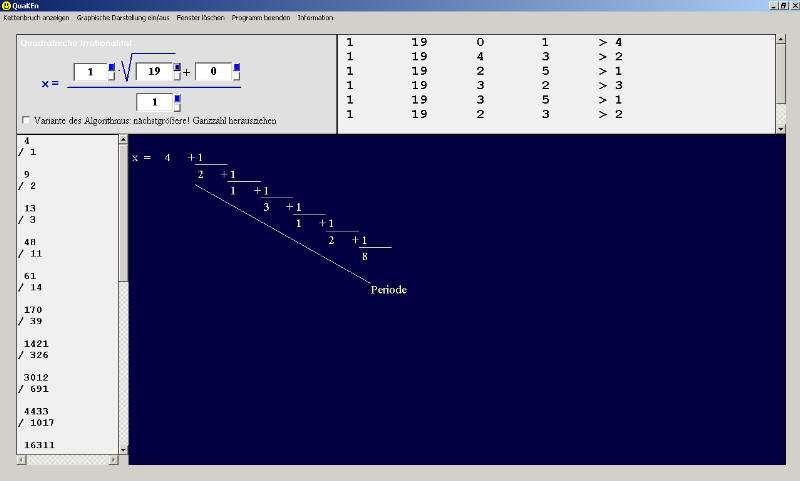
Die Programmoberfläche
Es handelt sich um Freeware. Das Programm kann hier heruntergeladen werden.
2. Visualisierung der Approximationsgüte, Pellsche Gleichungen und Bruchfolgen
Für die gewählte quadratische Irrationalität werden für jeden Nenner die am besten approximierenden Brüche angezeigt. Die erreichte Genauigkeit wird durch einen Stammbruch und durch das Absolutglied der vom approximierenden Bruch gelösten Pellschen Gleichung angegeben.
Man kann sich mit diesem Programm Material zur Mustersuche bezüglich der oben aufgeworfenen Fragen beschaffen.
Durch die Visualisierung kann man aber auch die durch gängige Approximationsverfahren (Heron, Pellsche Gleichungen oder Kettenbrüche u. a.) erreichbare Qualität und Konvergenzgeschwindigkeit plastisch darstellen. Dabei kann man tiefere zahlentheoretische Muster entdecken und sich Datenmaterial für eigene Vermutungen und Beweise beschaffen.
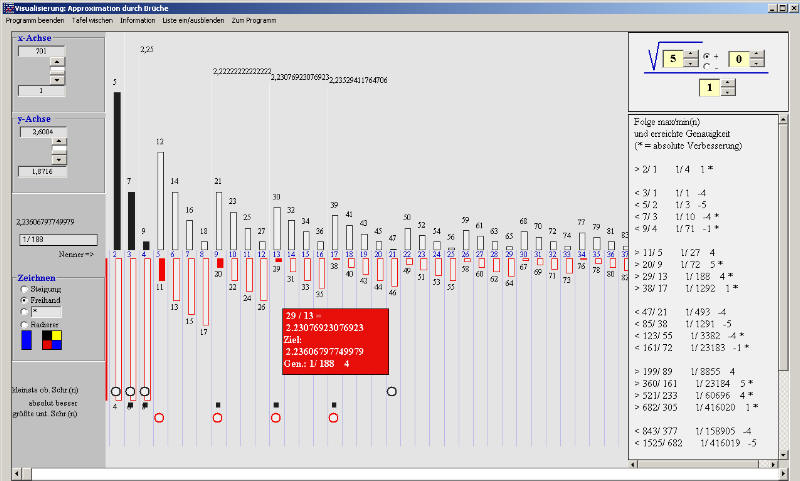
Beispiel: Der Bruch x/y = 29/13 approximiert √5 mit einer Genauigkeit von ca. 1/188
und löst die Pell'sche Gleichung 5y2 = x2 + 4