| Hauptseite |
Zur Konstruktion nichttransitiver extremaler Efron-Würfel-Ringe |
||||||||||||||||||||||||||||
|
|
Beitrag in den Mitteilungen der
Mathematischen
Gesellschaft Hamburg
|
Wie hoch kann die kleinste in einem Würfelring aus n Würfeln vorkommende Gewinnwahrscheinlichkeit für jede Seitenzahl k durch geschickte Verteilung von Augenzahlen auf die Seiten der beteiligten Würfel getrieben werden? |
|||||||||||||||||||||||||||
| Bericht über die Entwicklung einer Mini-Theorie im Hamburger Projekt zur Begabtenförderung. | |||||||||||||||||||||||||||||
|
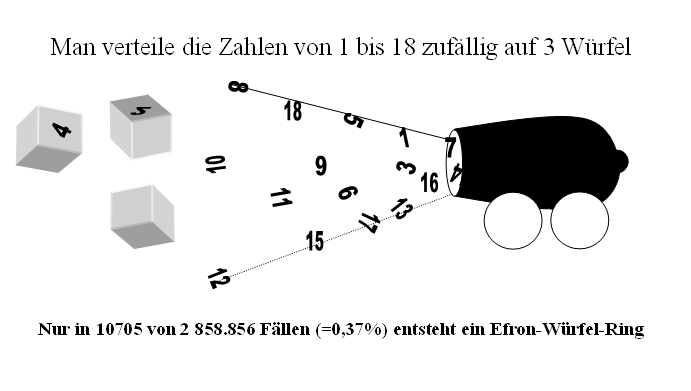
Das Würfelset von Bradley Efron ist in dem Sinne "kurios", dass es gegen ein Denkmuster verstößt: Die besser-als-Relation ist hier nicht transitiv. Dabei wird ein Würfel X "besser als" ein Würfel Y genannt, wenn beim gleichzeitigen Werfen beider Würfel die Wahrscheinlichkeit dafür, dass X eine höhere Zahl als Y zeigt, größer ist, als für den umgekehrten Fall. Man findet nun zu jedem der vier Würfel einen besseren! Auf allen Würfeln ist die Summe der Augenzahlen zudem gleich, nämlich 36. Indem man für je zwei im Ring benachbarte Würfel alle 36 möglichen Kombinationen von Augenzahlen ansieht, findet man, dass die Gewinnwahrscheinlichkeit stets 2/3, also 66% beträgt. Man kann an die Penrose-Treppe denken, bei der es nur bergauf geht:
Das folgende Ergebnis einer kombinatorischen Abzählung zeigt, dass Efron-Würfel-Ringe in gewisser Weise etwas Seltenes sind:
Das von Efron angegebene Set aus drei Würfeln kann in ein Set transformiert werden, in dem alle Zahlen von 1 bis 24 genau einmal vorkommen:
↓ (fortlaufende Ersetzung von klein zu groß)
Leider sind die Augensummen auf den einzelnen Würfeln nun nicht mehr gleich. Eine der Bedingungen (fortlaufende Numerierung / gleiche Augensummen) ist für gewisse interessante Fälle immer realisierbar, beide gleichzeitig sind jedoch nicht immer realisierbar. |
|||||||||||||||||||||||||||||
|
Im Hamburger Projekt zur Begabtenförderung haben wir die folgende Forschungsfrage gestellt:
Kann die durch Efrons Beispiel gegebene Kuriosität durch besonders geschickte Verteilungen der Augenzahlen noch extremer gemacht werden? Dabei wollen wir - um den Kombinationsreichtum zu vergrößern - zwei Verallgemeinerungen vornehmen:.
Betrachtet werden nicht nur "herkömmliche Würfel", sondern alle Sets aus n k-seitigen "allgemeinen Würfeln" (man kann an Glücksräder denken, bei denen man ja nicht auf 6 Seiten beschränkt ist oder - für gewisse Fälle - an platonische und archimedische Körper). |
|||||||||||||||||||||||||||||
| 2. Exploratives | |||||||||||||||||||||||||||||
|
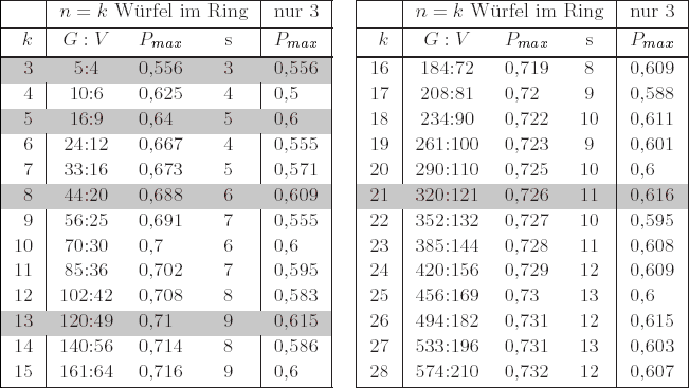
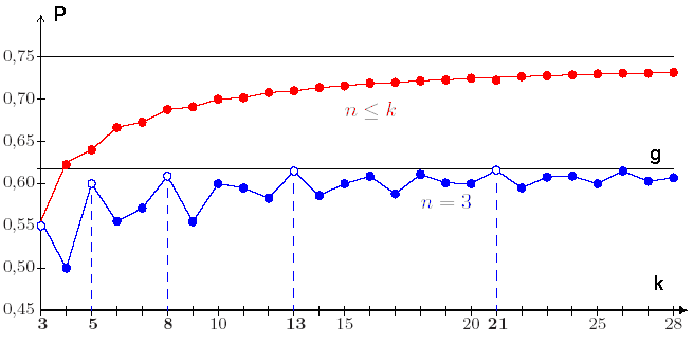
Die Tabelle zeigt die höchsten zu realisierenden Gewinnwahrscheinlichkeiten Pmax für die schwächste Stelle im Efron-Würfel-Ring aus n k-seitigen Würfeln. Auffällig ist die besondere Rolle der Fibonacci-Zahlen (wenn man nur drei Würfel nimmt läuft P auf die kleine Goldene Schnittzahl zu) und die monotone Approximation an P = 75% wenn man bis n=k k-seitige Würfel erlaubt.
Wie man sieht, zahlt sich die Erhöhung der Seitenanzahl k aus. Man hat mehr Möglichkeiten zur "Feinabstimmung" bei der Würfelbeschriftung und kann daher die kleinste im Ring vorkommende Gewinnwahrscheinlichkeit vergrößern (rote Kurve; man darf bis zu k Würfel verwenden). Die Kurve nähert sich asymptotisch an 3/4. Dies ist für beliebig viele Würfel mit beliebig vielen Seiten die nicht erreichbare Obergrenze. Besteht der Würfelring aus nur drei Würfeln, so erreicht man besonders hohe Gewinnwahrscheinlichkeiten an der schwächsten Stelle, wenn k eine Fibonaccizahl ist (danach fallen sie wieder unter den erreichten Wert und übertreffen ihn erst wieder bei der nächsten Fibonaccizahl). Diese Gewinnwahrscheinlichkeiten nähern sich der kleinen Goldenen-Schnitt-Zahl.
|
|||||||||||||||||||||||||||||
| Ein Beispiel zur Einführung einer besonderen graphischen Repräsentation: | |||||||||||||||||||||||||||||
|
Der Würfelring W1= {1, 2, 9, 14, 15, 16}, W2 = {6, 7, 8, 11, 12, 13}, W3 = {3, 4, 5, 10, 17, 18}, hat hohe Gewinnwahrscheinlichkeiten und zwei weitere Besonderheiten. Jede der Zahlen von 1 bis 18 kommt genau einmal vor und jeder Würfel trägt dieselbe Augensumme, nämlich 57. Die Berechnung der Gewinnwahrscheinlichkeiten kann mit einer Tabelle übersichtlich durchgeführt werden:
Dieser Würfelring kann graphisch so dargestellt werden: Die Speichen repräsentieren die Würfel. Die Augenzahlen sind der Größe nach geordnet aufgetragen. Von jeder Augenzahl jedes Würfels wird ein Bogen zu der größten Augenzahl des Ringnachfolgers gezogen, die noch geschlagen wird. Diese Repräsentation ist mathematisch und psychologisch vorteilhaft, denn sie spiegelt die zyklische Struktur der Efron-Würfel-Ringe wider und nimmt - da man die Zahlen weglassen kann - automatisch eine Äquivalenzklassenbildung vor. |
|||||||||||||||||||||||||||||
| Mit Hilfe dieser Darstellung können einige Sätze der kleinen Theorie leicht bewiesen werden (näheres im Artikel oben). | |||||||||||||||||||||||||||||
|
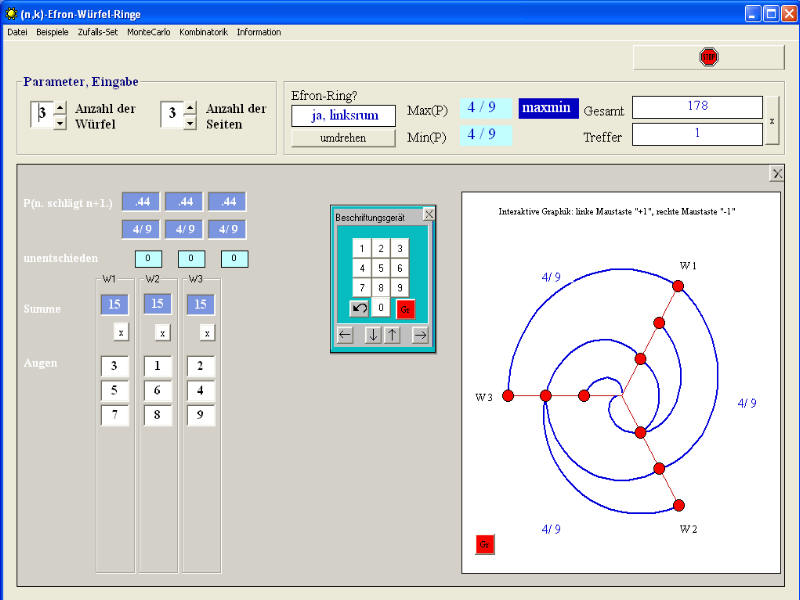
Mit Hilfe eines kleinen Computerprogramms (400KB) können eigene Untersuchungen durchgeführt werden. Man wählt, wie viele Würfel man haben möchte und die Seitenzahl der Würfel. Dann beschriftet man die Seiten. Das Programm berechnet die Gewinnwahrscheinlichkeiten benachbarter Würfel. Man kann also mit verschiedenen Beschriftungen experimentieren und sich spielerisch einen Einblick in die kombinatorischen Möglichkeiten verschaffen. Darüber hinaus kann man mit Hilfe der Monte-Carlo-Methode nach solchen Würfel-Ringen suchen lassen (Versuche- und Trefferstatistik wird ausgegeben) oder exakte Zählverfahren nutzen. |
|||||||||||||||||||||||||||||
|
download des Programms (184KB) (reine exe-Datei) download eines Installationsprogramms (überflüssig aber bequem, da es gleich eine Programmgruppe anlegt) |
|||||||||||||||||||||||||||||
| Impressum | |||||||||||||||||||||||||||||
| Link zur Institutsseite: | Dr. Hartmut Rehlich, IDM Braunschweig, Bienroder Weg 97, 38106 Braunschweig | ||||||||||||||||||||||||||||
|
Die übliche Bitte: Sollten dem Leser dieser Seiten Fehler in Orthographie, Sinn und Verstand auffallen, so bittet der Verfasser um Nachsicht und Nachricht und bittet auch darum, die Tücken der Technik (auf die auch andere hingewiesen haben) zur Entschuldigung ins Kalkül zu ziehen:
|
O unberachenbere
Schreibmischane,
--- Du tappst die
falschen Tisten, luber Bieb! von J. Guggenmoos |
||||||||||||||||||||||||||||