|
Das 15er Spiel auf beliebigen Spielgraphen |
||||||||
|
|
Artikel für den Tagungsband der |
Eine durch die starre Schiebemechanik des Ausgangsspiels vorgegebene Einschränkung wird aufgelöst |
||||||
|
|
||||||||
|
Skizze zur Entwicklung einer kleinen elementarmathematischen Theorie und ein Computerprogramm zum Spielen, Nachvollziehen und für eigene weiterführende Erkundungen |
||||||||
|
▼ ▲ Der Inhalt dieser Seite: 1. Das Spiel- und Untersuchungswerkzeug: Graphen-Boss-Puzzle 2. Zur Geschichte der Theorieentwicklung 3. Die Anzahl der Äquivalenzklassen beim Boss-Puzzle 4. Die Beweisanalyse deutet auf allgemeinere Zusammenhänge 5. Achtergraphen - die Charakterisierung sinnvoller und nichttrivialer Spielgraphen 6. Schöne Nebensätze, die in der fertigen Theorie untergehen 7. Zwei theorieerzeugende Basisoperationen 8. Die Bestimmung der Anzahl von Äquivalenzklassen auf Achtergraphen 9. Zusammenfassung und Vorstellung des Einsiedlergraphen 10. Das Boss-Puzzle auf beliebigen elementaren Spielgraphen
|
||||||||
| ▼ ▲ 1. Das Spiel- und Untersuchungswerkzeug: Graphen-Boss-Puzzle | ||||||||
|
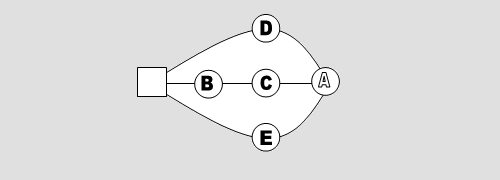
Mit dem Computerprogramm (Abb. 1 zeigt die Oberfläche) kann man beliebige Spielgraphen erstellen und auf diesen spielen. Zuerst plaziert man mit "drag and drop" die Felder (Aktion 1 anklicken), dann zieht man die Verbindungen (Aktion 2 anklicken), dann startet man das Spiel (Aktion 3 anklicken). Die Ampel oben links schaltet von rot auf grün und man kann spielen. Klickt man dem leeren Feld benachbartes Feld an, so bewegt sich der Spielstein von diesem Feld auf das Leerfeld. Gibt es danach nur eine Möglichkeit, wie es sinnvoll weitergeht, so wird dieser Zug automatisch gemacht, falls "Kaskade" aktiviert ist. Die Spielsteine, die Spielfelder und der Hintergrund können beliebig gefärbt werden (mit der rechten Maustaste anklicken). Die Spielsteine können beliebig beschriftet werden.
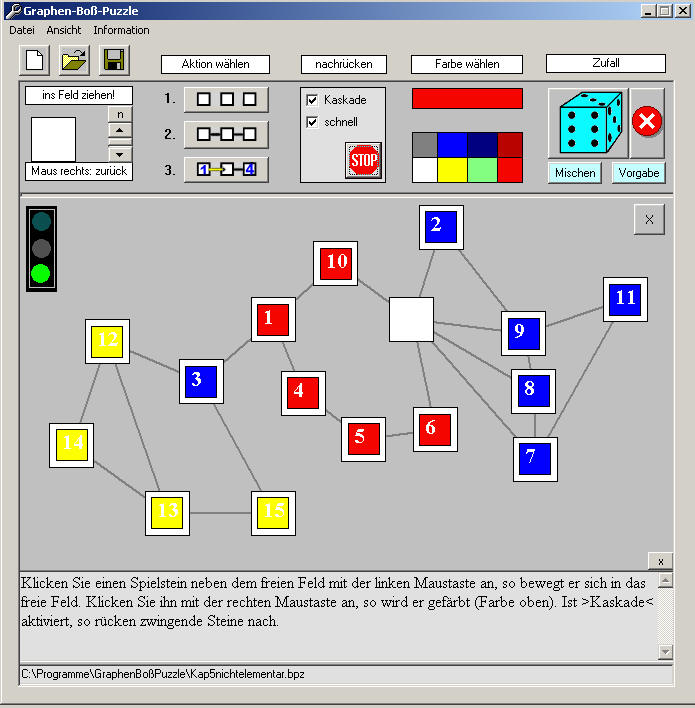
Abb. 1
download des Installationsprogramms (Freeware)
|
||||||||
|
In den frühen 1990er Jahren wurde das hier vorgestellte Problemfeld in der Oberstufengruppe des Hamburger Projekts zur Begabtenförderung bearbeitet. Die Bearbeitung einzelner Fragestellungen zu speziellen Graphen (insbesondere natürlich zunächst zum "handelsüblichen 15er-Spiel") weitete sich schnell auf beliebige Spielgraphen aus. In den folgenden Abschnitten werden einige wesentliche Ergebnisse dieser Beschäftigung zusammenfassend dargestellt.
|
||||||||
| ▼ ▲ 3. Die Anzahl der Äquivalenzklassen beim Boss-Puzzle | ||||||||
|
Beim Bosspuzzle - es ist auch als so genanntes 15er-Spiel bekannt - ist ein Feld in dem 4x4-Quadrat freigelassen. Der Rahmen enthält nur 15 verschiebbare Plättchen mit Zahlen. Die Lücke erlaubt es, ein benachbartes Plättchen in diese Lücke schieben. Dadurch entstehen neue Schiebemöglichkeiten. Das Spiel besteht darin, eine vorher festgelegte Endstellung herzustellen. Dabei steht man vor der Frage, welche Zielstellungen sich überhaupt herstellen lassen.
Abb. 2 Bei Spielausführungen mit herausnehmbaren Plättchen (bei den meisten handelsüblichen Plastikausführungen geht das nicht), kann man die Frage auch andersherum stellen: Man nimmt die Plättchen heraus, mischt sie, legt sie wieder ins Feld und versucht, die Ausgangsstellung durch Schiebeoperationen wiederherzustellen. Dabei steht man vor der Frage, welche Anordnungen man wieder in die Ausgangsstellung überführen kann. Die beiden Fragen sind natürlich gleichwertig, sie verhalten sich zueinander wie der Hin- und der Rückweg durch ein Labyrinth, gibt es einen Hinweg, so gibt es natürlich auch einen Rückweg und umgekehrt, da jeder Einzelschritt umkehrbar ist. Es ist bekannt (vgl. Ahrens 1901, Mathematische Unterhaltungen und Spiele, Teubner, Leipzig), dass es beim üblichen Boss-Puzzle zwei Äquivalenzklassen von Belegungen gibt. Es ist nicht möglich, bei dem Spiel beispielsweise die Steine mit den Zahlen 1 und 5 zu vertauschen. Die Belegungen liegen in verschiedenen Äquivalenzklassen. Dabei nennen wir zwei Belegungen genau dann äquivalent, wenn sie durch Schiebeoperationen im Sinne der als bekannt vorausgesetzten Spielregel ineinander überführbar sind. Wir „normieren“ die Darstellungen noch, indem wir das Leerfeld stets unten rechts verorten. Die schon bei Ahrens stehenden Ergebnisse werden hier in knapperer Form vorgestellt und bewiesen.
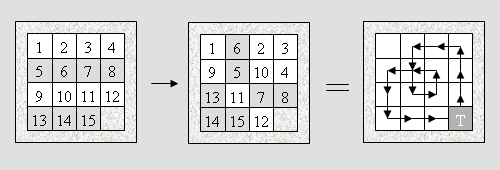
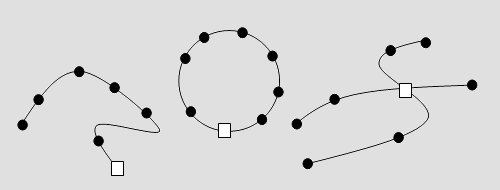
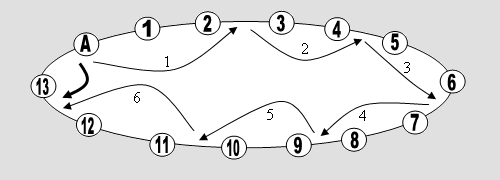
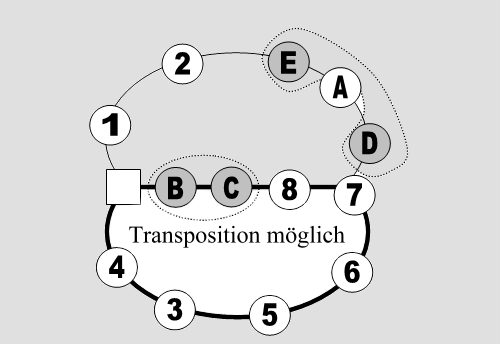
Satz 1 Beim normalen Bosspuzzle gibt es mindestens zwei Äquivalenzklassen von Belegungen. Beweis Wir nehmen eine Umdeutung vor: Das Schieben eines Steines in eine Lücke wird als Tausch mit dem Tauschstein T interpretiert. Dieser vollführt also eine Wanderung in dem Spielfeld und verändert dadurch die Anordnung der Steine (Bild 1). Ist er am Ende wieder unten rechts (normierte Lage), so ist er jedenfalls ebenso oft nach links, wie nach rechts und nach oben, wie nach unten bewegt worden. Er hat folglich eine gerade Anzahl von Schritten hinter sich (Abb. 3).
Abb. 3 Da jeder Schritt eine Transposition mit einem Zahlstein bewirkt (der Begriff Transposition wird hier im üblichen Sinne verwendet), können also nur gerade Permutationen erzeugt werden ■
Anmerkung zur Arbeit in unserer Fördergruppe: Dieser Satz aus der Gruppentheorie war unseren Teilnehmern nicht bekannt. Die gründliche Erarbeitung und Besprechung dieser Einsicht war eine besonders wichtige Voraussetzung für die Bearbeitung des allgemeineren Falls. Diese Einsicht ist auch ohne „strukturmathematisches Vorratswissen“ leicht zugänglich. In unserer Fördergruppe reichte es aus, in einer Sitzung (eine solche dauert in der Regel ca. 3 Stunden) die Idee einer „Zielabstandsfunktion“ einzugeben. Diese ordnet einer Belegung des Graphen mit Spielsteinen einen Abstandswert hinsichtlich der angestrebten Zielstellung zu. Diese Abstandsfunktion ist natürlich die Anzahl der Fehlstellungen.
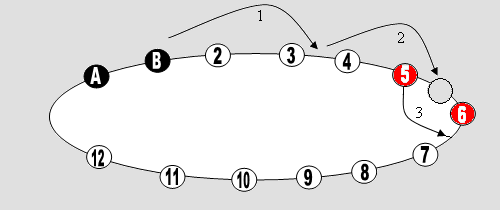
Satz 2 Beim normalen Bosspuzzle gibt es höchstens zwei Äquivalenzklassen von Belegungen. Beweis Wir streichen einige Kanten des Spielgraphen. Dadurch kann sich die Anzahl der Äquivalenzklassen nur erhöhen, aber nicht verringern.
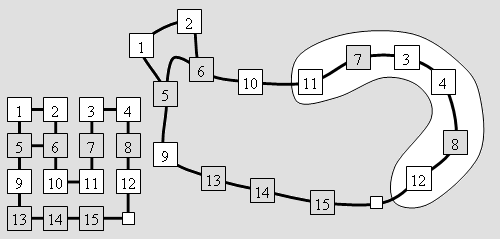
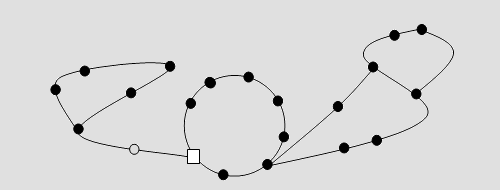
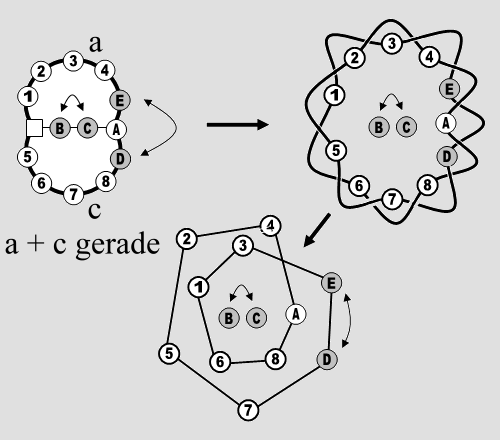
Abb. 4 Rechts in Abb. 4 wurde der Graph zusätzlich verformt. Diese gleichwertige Darstellung des Spiels macht die Entdeckung einer einfachen Beweisidee besonders leicht: Man sieht ja, dass die Steine in dem unteren Teilkreis wie ein Güterzug mit vielen Anhängern im Kreis bewegt werden können und die Steine mit den Nummern 1 und 2 unbehelligt oben „parken“. Die Steine des unteren Kreises laufen also an diesen vorbei. Möchte man nun im unteren Kreis eine bestimmte Reihenfolge erzeugen, so kann man iterativ vorgehen. Die umrandeten Steine seien bereits in der gewünschten Reihenfolge. Wir wollen nun zum Beispiel den Stein mit der Nummer 14 hinter den Stein mit der Nummer 11 bringen. Dann brauchen wir die 14 nur im oberen Bogen zu „parken“ und dann den „Güterzug“ auf dem unteren Kreis fahren zu lassen, bis der Stein mit der Nummer 14 an die 11 angehängt werden kann. Man überlegt sich leicht, dass dies immer möglich ist und man lediglich am Ende des Prozesses die Reihenfolge der beiden geparkten Steine so nehmen muss, wie sie sich ergibt. Sie können dann richtig (im Sinne eines vorgegebenen Zielzustandes) oder falsch stehen. Alle anderen stehen sicher richtig. Folglich gibt es höchstens zwei Äquivalenzklassen von Belegungen ■
|
||||||||
| ▼ ▲ 4. Die Beweisanalyse deutet auf allgemeinere Zusammenhänge | ||||||||
|
Wir sehen, dass es bei dem normalen Bosspuzzle genau zwei Äquivalenzklassen von Belegungen gibt und dass sich die Beweismethoden auf andere rechteckige Spielgraphen ebenso einfach anwenden lassen. Erste Ansätze zur Verallgemeinerung findet man bereits in dem genannten Werk von Ahrens. Dort werden z.B. Schranken im Puzzle gezogen, also Schiebemöglichkeiten weggenommen.
Ahrens, S. 363 Das folgende Bild 5 zeigt einen rechteckigen Spielgraphen und noch einen weiteren Spielgraphen, auf dem alle Rundwege des „Tauschsteins“ (wo immer dieser zur Normierung hingestellt wird) ebenfalls nur aus einer geraden Anzahl von Einzelschritten bestehen. Folglich gibt es auch bei diesen Spielgraphen mindestens zwei Äquivalenzklassen von Belegungen.
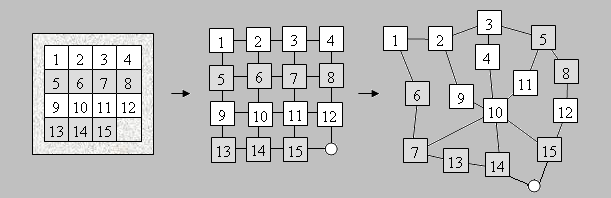
Abb. 5 Die im letzten Beweis vorgenommene Verformung des Graphen weist also den Weg zu der im Folgenden dargestellten Verallgemeinerung. Wir trennen uns von der starren Schiebemechanik und bringen das Spiel nun auf beliebige Graphen. Im Folgenden wird uns dabei die Frage beschäftigen, wie weit die vorgestellten Grundüberlegungen bei der Analyse beliebiger Spielgraphen reichen und welche weiteren Betrachtungen nötig sind um möglichst viele Spielgraphen "in den Griff zu bekommen". Diese Verallgemeinerung geht weit über die bei Ahrens angesprochene Verallgemeinerung hinaus, bei der nur Spielfelder betrachtet werden, die man als Teilfelder vollständiger rechteckiger Spielfelder betrachten kann.
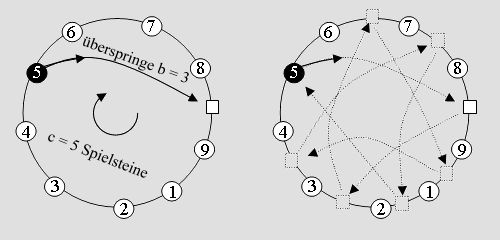
Ahrens, S. 365 Bei Graphen dieser Art bestehen alle Teilkreise aus einer geraden Anzahl von Feldern und Ahrens betrachtet nur Beispiele, die eine "Parkbucht" enthalten, mit deren Hilfe man in einem Kreis zwei Felder überspringen kann:
zur Verallgemeinerung bei Ahrens S. 365 Diese Möglichkeit zum "Zweisprung" sieht man leicht, wenn man die abgebildete Situation in der Weise auffasst, dass die Spielsteine zyklisch entlang des Außenkreises (fette schwarze Verbindungen) angeordnet sind. Dadurch, dass man den Spielstein mit der Nummer 2 nun entlang der "Abkürzung" (blaue Verbindung) bewegt, ist der Spielstein über die Spielsteine mit den Nummern 3 und 4 hinweggesprungen. Man kann sich nun überlegen, dass dies dazu führt, dass es höchstens zwei Äquivalenzklassen von Belegungen bei solchen Graphen geben kann. Da es jedoch auch mindestens zwei Äquivalenzklassen gibt (da es nur Kreise mit gerader Eckenzahl gibt), gibt es folglich für derartige Graphen stets genau zwei Äquivalenzklassen von Belegungen. Da weiter unten ähnliche Überlegungen für einen allgemeineren Fall dargestellt werden, soll es hier bei dieser knappen Beschreibung bleiben.
|
||||||||
| ▼ ▲ 5. Achtergraphen | ||||||||
|
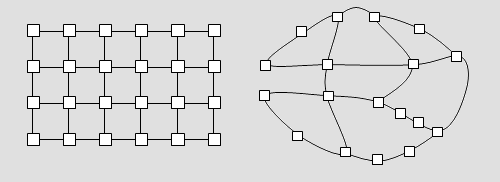
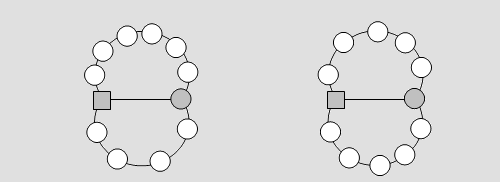
Es ist unmittelbar klar, dass das Spielen auf Bäumen und Kreisen langweilig und die Frage nach der Anzahl der Äquivalenzklassen von Belegungen trivial ist (das Quadrat auf den Spielgraphen in Abb. 6 deutet das freigelassene Feld an, alle anderen denke man sich mit numerierten Spielsteinen belegt, diese werden im Folgenden nur dann mitgezeichnet, wenn sie wichtig sind). Auf dem Graphen links gibt es 6! = 720 Äquivalenzklassen, auf dem Kreisgraphen ebenfalls (man kann jeden der sieben Spielsteine auf ein beliebiges Feld stellen und muss die anderen dann so nehmen, wie sie sich ergeben) und auf dem Baum rechts gibt es 7! Äquivalenzklassen, denn man kann auch hier überhaupt nichts machen.
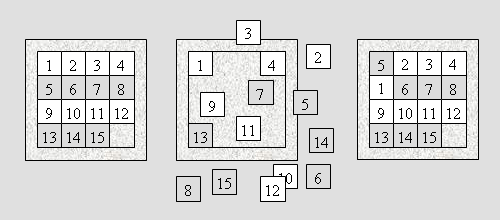
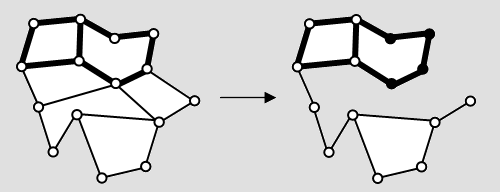
Abb. 6 Die Anzahl der Äquivalenzklassen in Spielgraphen, die nur einfach zusammenhängend sind, kann ganz offensichtlich leicht auf die Anzahl der Äquivalenzklassen in den „Teilgraphen“ zurückgeführt werden (Abb. 7).
Abb. 7 Die Spielsteine sind an ihre Teilgraphen „gefesselt“. Der Stein auf dem grau markierten Platz ist an die Brücke gefesselt. Kennt man die Anzahl der Äquivalenzklassen der Teilgraphen, so ist es nur noch ein einfaches Zählproblem, die Anzahl der Äquivalenzklassen für den ganzen Graphen zu bestimmen. Solche Zusammensetzungen sollen daher im Folgenden nicht weiter untersucht werden. Das eigentliche Problem besteht nämlich darin, die „elementaren Spielgraphen“ zu beherrschen.
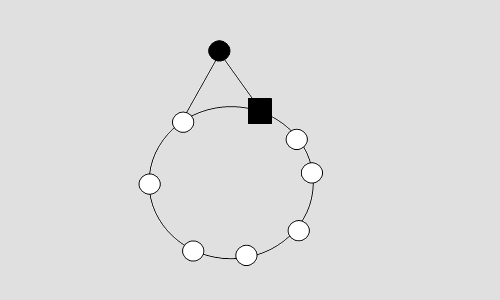
Elementare Spielgraphen Ein einfacher Kreis ist kein elementarer Spielgraph. Elementare Spielgraphen sind alle anderen Graphen, bei denen je zwei Ecken (Felder) die Ecken eines überschneidungsfreien kreisförmigen Untergraphen sind. Alternativ zur letzten Bedingung kann man auch fordern, dass jeder Spielstein durch Schiebeoperationen auf jedes Feld gebracht werden kann oder dass die Graphen zweifach zusammenhängend sind. ■ Anmerkung: Es ist klar, dass "Supergraphen", also solche, bei denen zwei Ecken durch zwei verschiedene Kanten verbunden sein können, uninteressant sind (dadurch ändert sich nichts am Spiel, man kann solche doppelten Kanten einfach weglassen).
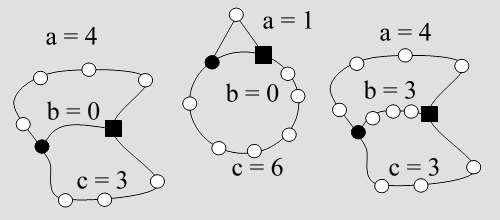
Definition „Achtergraph“ Die kleinsten elementaren Spielgraphen haben die Form eines Kreises mit Brücke, im Folgenden Achtergraph genannt, haben. Abb. 7 zeigt drei Achtergraphen. Man kann sie durch Zahlentripel charakterisieren:
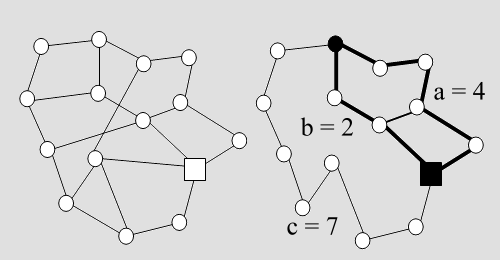
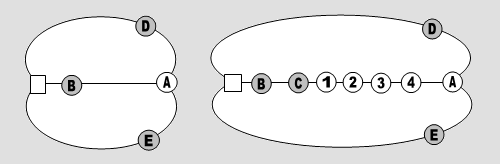
Abb. 7 So ein Achtergraph besteht also aus drei Bögen, die nur Felder mit dem Eckengrad 2 enthalten und zwei Ecken mit dem Eckengrad 3. Dort treffen die Bögen zusammen, in der Skizze wurde auf einem dieser Felder das Leerfeld postiert (das schwarze Quadrat steht für das Leerfeld). Ein Achtergraph kann durch ein Tripel (a, b, c) charakterisiert werden. Mindestens zwei der Parameter a, b und c müssen größer als Null sein. Die Gesamtzahl der Spielsteine ist also a + b + c + 1.■ Der Reiz der Achtergraphen Die Achtergraphen sind die kleinsten elementaren Spielgraphen. Wenn man über die Achtergraphen Bescheid weiß, hat man alle elementaren Spielgraphen "im Griff". Das wird durch den in Abb. 8 angedeuteten Reduktionsprozess nahegelegt (man denke daran, dass man auf einem beliebigen Bogen - wie im Beweis zu Satz 2 - stets jede beliebige Anordnung von Spielsteinen herstellen kann).
Abb. 8 Man fasse den rechts abgebildeten elementaren Spielgraphen also zunächst als einen (4. 2, 7) Achtergraphen auf und belege den 7er Bogen in der gewünschten Weise. Danach kümmere man sich um den fett hervorgehobenen (4, 0, 2) Achtergraphen. Der Ausgangsgraph hat also höchstens so viele Äquivalenzklassen von Belegungen, wie dieser Untergraph.
|
||||||||
| ▼ ▲ 6. Schöne Nebensätze, die in der fertigen Theorie untergehen | ||||||||
|
Wie weiter oben schon bemerkt wurde, ist die Entwicklung einer kleinen Theorie in der Regel kein linearer Vorgang. Die in diesem Abschnitt vorgestellten Erkenntnisse wurden im Laufe der Bearbeitung durch allgemeinere Einsichten ergänzt und werden zur Darstellung unserer Theorie eigentlich nicht mehr benötigt. Innerhalb des Findungsprozesses waren sie aber nicht zuletzt aus zwei Gründen „psychologisch wichtig“. Einerseits ermunterten diese kleinen Erfolgserlebnisse unsere Teilnehmer zum Weitermachen und andererseits ebneten sie vielleicht auch erst den Weg zu komplexeren Einsichten.
Nebensatz 1 Auf Achtergraphen mit a=0, b=1 und beliebigem c gibt es nur eine Äquivalenzklasse von Belegungen.
Abb. 9 Beweis Der auf dem runden schwarzen Feld "geparkte Stein" kann ganz offensichtlich an jeder Stelle eingefügt werden. Entsprechendes gilt auch für alle anderen Spielsteine, da jeder Spielstein dort abgestellt werden kann. ■
Nebensatz 2 Auf Achtergraphen mit a=0 und ggT(b, c) = 1 gibt es nur eine Äquivalenzklasse von Belegungen.
Abb. 10 Beweis Wir repräsentieren die Situation anders, nämlich als "Kreisverkehr" in Abb. 10, bei dem ein Stein b Steine durch die „Abkürzung“ (den 0-Bogen) überspringen kann. Es ist klar, dass dies mehrfach iteriert werden kann (sobald sich alle Spielsteine um c Plätze weiterbewegt haben, ist dieser Stein wieder an der Abzweigung. Es gibt insgesamt b+c Lücken zwischen den anderen Spielsteinen. ist b teilerfremd zu b+c, so kann also jede Lücke aufgesucht werden (man kann hier daran denken - und das auch analog begründen - , dass in der additiven Restegruppe modulo b + c jede zu b + c teilerfremde Zahl durch fortgesetzte Addition die gesamte Gruppe erzeugt). Damit kann im durch Abb. 10 gegebenen Beispiel der Spielstein mit der Nummer 5 an jede beliebige Stelle rangiert werden. Da gleiches für alle Steine gilt, gibt es nur eine Äquivalenzklasse von Belegungen. ■
Nebensatz 3 Auf Achtergraphen mit a=0 und beliebigem b>0 und c>0 gibt es höchstens (min {b, c})! Äquivalenzklassen von Belegungen. Beweis Es handelt sich um eine einfache Verallgemeinerung der Überlegungen zum Beweis von Satz 2. ■
|
||||||||
| ▼ ▲ 7. Zwei theorieerzeugende Basisoperationen | ||||||||
|
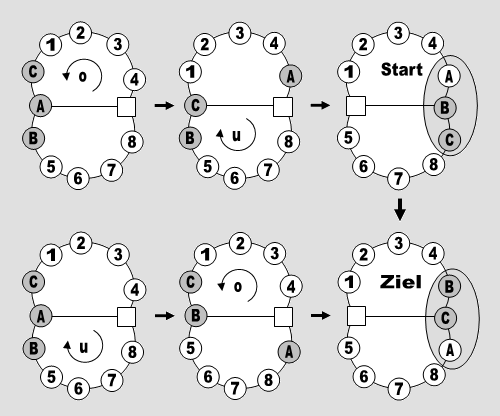
Die durch die Nebensätze gewonnenen Abschätzungen sind sehr speziell oder zu grob. Wer sich seinerzeit mit dem farbigen Drehwürfel, dem sogenannten Rubikwürfel beschäftigt hat, erinnert sich sicher daran, dass bei der Untersuchung von Strukturen in Permutationsgruppen - und darum handelt es sich ja auch hier - die Betrachtung geschickt gewählter "zusammengesetzter Elementaroperationen" äußerst nützlich sein kann. So wird nun auch hier vorgegangen. Die folgenden beiden Hilfssätze führen die entscheidenden Analysewerkzeuge ein. Bei ihnen handelt es sich um die in Abschnitt 2 schon angesprochenen „Superzeichen“ oder „Superoperationen“, die als neue Einheiten das mühsame, ermüdende und schnell zu Konfusionen führende „Denken in Einzelschritten“ durch ein spielerisches Denken in größeren Einheiten ablösen. Die Vorstellung dieser Superoperationen folgt der Methode ihrer Entdeckung. Unter Zuhilfenahme eines kleinen Computerprogramms wurden – ausgehend von der immer gleichen Startkonstellation – leicht unterschiedliche Handlungsfolgen ausgeführt. Diese erzeugen leicht unterschiedliche Anordnungen der Spielsteine und es ist klar, dass diese leicht unterschiedlichen Belegungen dann ihrerseits ineinander überführbar sind (alle Schiebeoperationen sind umkehrbar). Im Bild zu Hilfssatz 1 rücken zunächst die Steine im oberen Bogen (o) zyklisch und gegen den Uhrzeigersinn um je eine Position weiter, dann rücken die Steine im unteren Bogen (u) zyklisch und im Uhrzeigersinn eine Position weiter. In der Zeile darunter ist zu sehen, welche Wirkung es hat, wenn man die Reihenfolge dieser Operationen vertauscht.
Hilfssatz 1 Auf einem Achtergraphen mit a = 0 und b, c ≥ 2 kann jeder Stein über zwei Nachbarn hinwegspringen (die lokale Anordnung ABC in Abb. 11 kann in BCA transformiert werden.
Abb. 11 Beweis Das abgebildete Beispiel ist "paradigmatisch". Die vorgestellten Operationen sind mit allen Achten möglich, bei denen a=0 (in Abb. 11 der mittlere Bogen) und b, c ≥ 2 gilt. Um von der Anordnung oben rechts zur Anordnung unten rechts zu gelangen (bei der alle Spielsteine bis auf A, B, und C liegen geblieben sind), muss man die Reihenfolge der Operationen in der oberen Zeile natürlich umkehren, d.h. die Gegenoperationen durchführen und dann die Operationen in der unteren Zeile durchführen. ■
Anmerkung: Wir sehen hier, dass der schon oben angesprochene Zweisprung für den speziellen Fall, dass eine der Bogenlängen gleich 2 ist, immer möglich ist, wenn nur ein 0-Bogen vorhanden ist (ist b = 1 oder c = 1, so gibt es nach Nebensatz 1 ohnehin nur eine Äquivalenzklasse, daher ist dann trivialerweise auch ein Zweisprung möglich, das ist aber uninteressant).
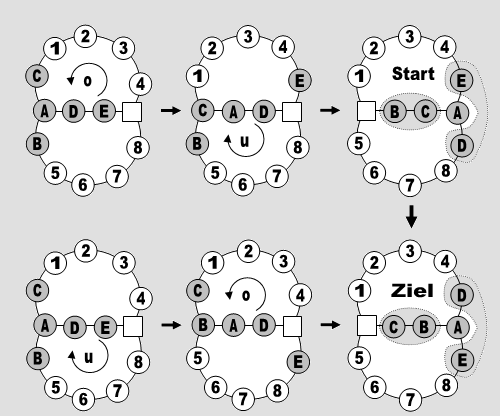
Hilfssatz 2 Auf einem Achtergraph mit a ≥ 2 und b, c ≥ 1 kann auf einem Bogen eine Transposition (Nachbarschaftstausch) und auf dem Kreis aus den beiden anderen Bögen ein Tausch mit dem übernächsten Nachbarn vorgenommen werden.
Abb. 12 Beweis Auch hier kehrt man die Operationen in der oberen Zeile wieder um und führt dann die Operationen in der unteren Zeile durch. Der in der Graphik mittlere Bogen muss mindestens zwei Plätze haben. Da a ≥ 2 gilt, kann man diesen Bogen in die Mitte nehmen und damit die Bedingung erfüllen. Stehen in der Startbelegung zwischen C und A noch weitere Steine auf weiteren Ecken, so behalten auch diese bei der Operation ihre angestammten Plätze.■
Den kleinsten Achtergraphen, bei dem diese Operation möglich ist, zeigt Abb. 13.
Abb. 13
|
||||||||
|
Hilfssatz 1 beschreibt eine Basisoperation, mit deren Hilfe man die Anzahl von Äquivalenzklassen auf Achtergraphen mit einem Nullbogen leicht bestimmen kann. Wir repräsentieren dazu das Spiel etwas anders: n Spielsteine seien ringförmig angeordnet. Diese können dadurch umsortiert werden, dass ein beliebiger Stein zwei Nachbarsteine überspringt (wir lassen also die „Brücke“ weg und arbeiten mit dem „Superzeichen“ 2-Sprung aus Hilfssatz 1).
Abb. 14 Die 6 Zweiersprünge ergeben im Resultat also einen Rückwärtssprung um eine Position. Man kann also zwei benachbarte Steine vertauschen. Damit ist aber jede Belegung herstellbar. Dass dies im Beispiel funktioniert, liegt offensichtlich daran, dass die Anzahl der Gesamtsteine gerade ist. Dies beweist den folgenden Hauptsatz.
Hauptsatz 1 Auf Achtergraphen mit a = 0 und b, c ≥ 2 und b+c ungerade, gibt es genau eine Äquivalenzklasse von Belegungen (die Gesamtzahl an Spielsteinen ist a + b + c + 1, also gerade).■
Nun möchte man natürlich wissen, wie die Verhältnisse sind, falls b+c gerade ist. Eine einfache Transposition ist dann in der skizzierten Weise nicht herstellbar. Es kann also mehr als nur eine Äquivalenzklasse von Belegungen geben. Der nächste Satz stellt klar, dass es jedoch nicht mehr als zwei Äquivalenzklassen von Belegungen geben kann.
Hauptsatz 2a Auf Achtergraphen mit a=0 und b, c ≥ 2 und geradem b+c (die Gesamtzahl an Spielsteinen ist a + b + c + 1, also ungerade) , gibt es höchstens zwei Äquivalenzklassen von Belegungen.
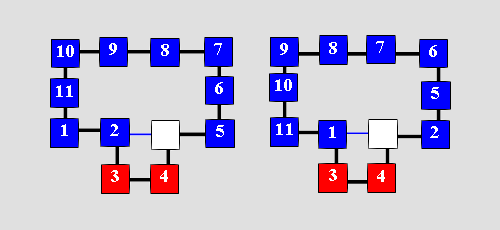
Beweis Wir zeigen, dass - bis auf zwei vorher ausgewählte Steine, die sogenannten "schwarzen Böcke", die nicht involviert werden - jeder Stein mit seinem direkten Nachbarn vertauscht werden kann. Im folgenden Bild sind A und B die Böcke und wir wollen die Steine 5 und 6 vertauschen.
Abb. 15 Zunächst springen wir mit einem der Böcke (das ist mit „Zweisprüngen“ immer möglich, da es ja zwei benachbarte Steine sind) zwischen die zu tauschenden Steine. Dann vollführen wir mit einem dieser Steine einen Zweisprung (im Bild ist das Sprung 3). Danach springt der Bock zu seinem Partner zurück. Das geht immer, er landet entweder auf seiner rechten oder linken Seite. Im Effekt ist Stein 5 über seinen Nachbarn gesprungen. Folglich kann man sämtliche Steine – bis auf die Böcke – in jede beliebige Reihenfolge bringen. Daher gibt es höchstens zwei Äquivalenzklassen von Belegungen (das sind eben die beiden Möglichkeiten, wie die Böcke stehen können)■
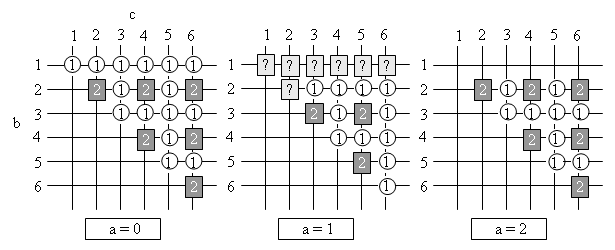
Damit hat man die Achtergraphen mit einem unbelegten Bogen weitgehend im Griff. Man muss nur noch die Frage klären, wann es genau zwei Äquivalenzklassen von Belegungen auf diesen Achtergraphen gibt. Dazu betrachten wir die Achtergraphen mit geradem b+c einmal etwas genauer. Es gibt zwei Möglichkeiten: Entweder sind beide Zahlen gerade oder beide Zahlen sind ungerade. Falls beide Zahlen gerade sind, ist der Fall klar. Dann gibt es nämlich nur gerade Rundwege für den „Tauschstein“ (vgl. Satz 1) und somit gibt es mindestens zwei Äquivalenzklassen von Belegungen. Der (0, 6, 4)-Achtergraph im folgenden Bild gibt ein Beispiel. Im anderen Fall kann man auch ungerade Permutationen herstellen. Da man aber alle geraden Permutationen ohnehin herstellen kann, kann man somit jede Permutation herstellen. Der (0, 5, 5)-Achtergraph im folgenden Bild gibt hierfür ein Beispiel.
Abb. 16 Hauptsatz 2b Auf Achtergraphen mit a=0 und b, c ≥ 2, gibt es genau dann genau zwei Äquivalenzklassen von Belegungen, wenn b und c gerade sind (die Gesamtzahl an Spielsteinen ist a+b+c+1, also ungerade) . Sonst gibt es nur eine Klasse. ■
Anmerkung: Diese Erkenntnisse gehen für bestimmte Parameterverhältnisse weit über die Erkenntnisse von Nebensatz 2 hinaus, dessen Beweis mit der hübschen „Idee des Kreisverkehrs“ arbeitet. Fasst man den (0, 5, 5)-Achtergraphen nämlich in der entsprechenden Weise auf, so kann ein Stein also immer nur 5 der 10 anderen Spielsteine überspringen, also letztlich nur zwischen zwei Plätzen ständig hin- und herwechseln (s. Bild 16). Man würde aus dem Blickwinkel der Beweismethode für Nebensatz 2 eine größere Anzahl von Äquivalenzklassen erwarten. Für andere Parameterverhältnisse, etwa für (0, 3, 7)-Achtergraphen, auf denen es ja auch nur eine Äquivalenzklasse von Belegungen gibt, ist allerdings der Nebensatz 2 viel eleganter als der Hauptsatz 2. Er beweist, dass Einklassigkeit eine ganz einfache Folge der Teilerfremdheit von 3 und 7 ist, während die zuletzt dargestellte Argumentation doch mit Sätzen der Gruppentheorie arbeitet. Wir haben nun also alle Achtergraphen mit einem Nullbogen „im Griff“ und wenden uns den Achtergraphen zu, bei denen alle Bögen Felder tragen. Hier werden einige Fallunterscheidungen wichtig, da die in Hilfssatz 2 beschriebene und hier zum Einsatz kommende Superoperation gewisse minimale Belegungszahlen für die einzelnen Bögen fordert. Dabei zeigt es sich, dass genau eine unendliche Klasse und ein Achtergraph durch das Netz der bisherigen Nebensätze, Hilfssätze und Hauptsätze fallen. Letzterer wird sich als singuläres Kuriosum innerhalb der Klasse der elementaren Spielgraphen erweisen. Doch zunächst wenden wir uns den weniger „exotischen Fällen“ zu.
Hauptsatz 3a Auf Achtergraphen mit a, b, c ≥ 2 gibt es höchstens zwei Äquivalenzklassen von Belegungen. Beweis Unter drei natürlichen Zahlen gibt es mindestens ein Zweierpaar mit gerader Summe. Die zugehörigen Bögen des (a, b, c)-Achtergraphen ordnen wir oben und unten an (a + c sei gerade).
Abb. 17 Nach Hilfssatz 2 können D und E und gleichzeitig B und C getauscht werden (alles andere bleibt fest). Im Außenkreis befindet sich eine ungerade Anzahl von Steinen. Wenn wir jeden Stein mit seinen übernächsten Nachbarn verbinden, entsteht also wieder ein Kreis, der alle Steine enthält (rechts im Bild). Die Superoperation aus Hilfssatz 2 bewirkt in diesem Kreis eine Vertauschung direkter Nachbarn. In diesem Kreis ist also jede Anordnung herstellbar (da man durch Drehen des gesamten Kreises links jedes gewünschte Paar in die Tauschposition bringen kann und diese Transposition daher an beliebiger Stelle vorgenommen werden kann), also auch in dem ursprünglichen Kreis. Falls der mittlere Bogen mehr als zwei Plätze hat, wird zunächst auf diesem Bogen die gewünschte Anordnung hergestellt, das geht ja immer (vgl. Beweis zu Satz 2). Folglich kann – im Hinblick auf eine beliebige Zielstellung – am Ende nur noch das Steinpaar (B, C) falsch stehen. Daher gibt es höchstens zwei Äquivalenzklassen von Belegungen. ■
Für die Argumentation ist es unverzichtbar, dass jeder Bogen mindestens zwei Felder trägt. Dadurch kann jeder Bogen die Rolle des mittleren Bogens in Bild 16 übernehmen und dadurch kann sichergestellt werden, dass man die Bögen mit der geraden Eckensummen außen herum hat. Durch Platz A wird die Anzahl der Spielsteine auf dem Außenbogen dann ungerade. Wir müssen den Fall, bei dem auf einem Bogen nur eine Ecke ist, also gesondert abhandeln.
Hauptsatz 3b Auf Achtergraphen mit a ≥ 3, b ≥ 2, c ≥ 1, gibt es höchstens zwei Äquivalenzklassen von Belegungen. Beweis Wir verwenden wieder die Operation aus Hilfssatz 2, allerdings in etwas anderer Art. Man kann bei Konstellationen der im folgenden Bild beschriebenen Art D mit E und C mit B tauschen, ohne den Rest zu ändern (man dreht den "Bumerang" so, dass der Stein A dort zu liegen kommt, wo im Bild die 7 ist und dreht nach erfolgter Operation den Außenkreis wieder zurück).
Abb. 18 Nun sei irgendeine Zielkonstellation vorgegeben. Zunächst belegt man den oberen Bogen in der gewünschten Art (einen Bogen kann man immer beliebig belegen). Dann sortiert man die Steine auf dem fett hervorgehobenen unteren Kreis, der aus den beiden unteren Bögen besteht, wie gewünscht. Das ist möglich, da man in diesem Kreis beliebige direkte Nachbarn tauschen kann (da man diese vorher durch das Drehen des gesamten Kreises auf die Positionen B und C stellen kann). Durch diesen Vorgang wird schlimmstenfalls die vorher auf dem oberen Bogen erzeugte Anordnung aller Spielsteine durch den Tausch der Nachbarsteine D und E zerstört (falls eine ungerade Anzahl von Sortierschritten für den unteren Kreis nötig ist). Folglich kann man bis auf die Reihenfolge von D und E, die man bei diesem Verfahren nehmen muss, wie sie sich ergibt, alle Gesamtkonstellationen herstellen. ■
Nun ist natürlich noch die Frage zu klären, unter welchen Bedingungen es für die von den Hauptsätzen 3a und 3b behandelten Achtergraphen genau zwei Äquivalenzklassen von Belegungen gibt. Man kann hier wieder völlig analog zum Beweis zu Hauptsatz 2b argumentieren und das Folgende feststellen:
Hauptsatz 3c Auf Achtergraphen mit a ≥ 3, b ≥ 2, c ≥ 1, oder a ≥ 2, b ≥ 2, c ≥ 2 gibt es genau dann genau zwei Äquivalenzklassen von Belegungen, wenn alle drei Summen a+b, a+c und b+c gerade sind (alle Rundwanderwege des Tauschsteins haben gerade Eckenzahl). Sonst gibt es genau eine Äquivalenzklasse von Belegungen. ■
Anmerkung An dieser Stelle des kleinen Theoriebildungsprozesses sind die Verhältnisse auf fast allen Achtergraphen geklärt. Bei den bisher betrachteten Achtergraphen gab es nur solche mit genau zwei und solche mit genau einer Äquivalenzklasse von Belegungen. Dabei haben genau jene, in denen alle Kreise (= Rundwanderwege des Tauschsteins) gerade Eckenzahl haben, genau zwei Klassen (was ja zunächst nur ein einfaches hinreichendes Merkmal für mindestens zwei Klassen ist).
|
||||||||
| ▼ ▲ 9. Zusammenfassung und Vorstellung des Einsiedlergraphen | ||||||||
|
Sichtet man alle Parameterkonstellationen überblicksartig, so fällt jedoch auf, dass noch einige wenige Fälle fehlen. Für die folgende grafische Darstellung wurden die drei Parameter der Größe nach sortiert (a ≤ b ≤ c) und als Koordinaten im dreidimensionalen Gitter gedeutet. Jeder Gitterpunkt repräsentiert also einen Achtergraphen und auf den Gitterpunkten steht die Anzahl der Äquivalenzklassen dieses Graphen.
Abb. 19 Schichten wir diese drei Ebenen nun übereinander, so sehen wir ein regelmäßiges räumliches Gitterpunktmuster vor uns (im Bild wurden die symmetrischen Fälle der Übersichtlichkeit zuliebe nicht eingetragen). Wie man sieht, sind allerdings noch „unendlich plus 1“ viele Fälle offen. Abb. 20 zeigt zwei Repräsentanten der unendlichen Serie.
Abb. 20 Der (1, 1, 1)-Achtergraph hat offensichtlich mindestens zwei Äquivalenzklassen von Belegungen (alle Kreise des Spielgraphen haben gerade Eckenzahlen) und er hat ebenso offensichtlich höchstens zwei Klassen. Das Muster wird also nicht gebrochen, auf (1, 1, 1) steht erwartungsgemäß wieder eine 2. Ebenso einfach erkennt man, dass die gesamte unendliche Serie sich bruchfrei einfügt. Sind auf dem mittleren Bogen nämlich wenigstens zwei Ecken, so kann die schon mehrfach verwendete Superoperation, die B mit C und gleichzeitig D mit E tauscht, ohne weitere Umsortierungen vorzunehmen, verwendet werden. Man belegt dann zunächst den mittleren Bogen in der gewünschten Weise und kann dann dafür sorgen, dass eines der genannten Paare richtig steht. So ergibt sich wieder die 2 als maximale Äquivalenzklassenzahl und analog zu schon geführten Beweisen der Hauptsatz 4: Hauptsatz 4 Die Anzahl der Äquivalenzklassen von Belegungen bei (1, 1, k)-Achtergraphen ist für ungerades k gleich 2 und sonst 1 ■
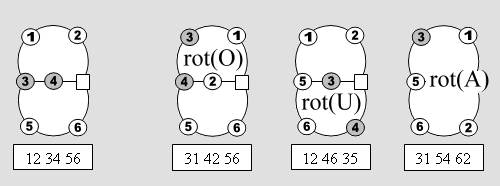
Ein ganz besonderer Fall: Der Einsiedlergraph Nun ist hinsichtlich der Achtergraphen nur noch der (1, 2, 2)-Achtergraph zu untersuchen. Unsere Teilnehmer und auch wir Betreuer hatten natürlich erwartet, dass auch dieser sich ohne Bruch in das symmetrische Ergebnismuster einfügt. Es ist jedoch überraschend, wie markant dieser Graph „aus der Reihe tanzt“, er hat als einziger Achtergraph sechs Äquivalenzklassen von Belegungen. Da man – wie in Abschnitt 3 schon angedeutet wurde – die Anzahl der Äquivalenzklassen von Belegungen sämtlicher Spielgraphen letztlich auf die Verhältnisse bei Achtergraphen zurückführen kann, ist er sogar der einzige elementare Spielgraph mit dieser Äquivalenzklassenzahl.
Hauptsatz 5 Der (1, 2, 3)-Achtergraph hat 6 Äquivalenzklassen von Belegungen. Wir nennen ihn im Folgenden „Einsiedlergraph“. Beweis Wir skizzieren knapp die Vorgehensweise einer kleinen Gruppe von Förderteilnehmern, die diesen Sachverhalt durch das Aufstellen einer Gruppentafel bewiesen. Dabei gingen sie geschickt vor. Es ist nämlich nicht ratsam, alle 6! = 720 Belegungen aufzuschreiben (es sind noch mehr, wenn man das leere Feld nicht zur Normierung an eine bestimmte Stelle setzt) und dann die Verknüpfungstafel aufstellt um dieser anzusehen, dass es 6 Teilmengen á 120 Belegungen gibt, die jeweils hinsichtlich der Übergänge abgeschlossene Einheiten bilden.
Abb. 21 Besser ist es, die Untergruppe „heranwachsen“ zu lassen. Dazu geht man von einer speziellen Belegung aus (Abb. 21, links). Es reicht nun zu betrachten, was geschieht, wenn man einen der drei Kreise im Uhrzeigersinn um eine Position weiterdreht. Dafür gibt es drei Möglichkeiten, die im Bild mit rot(O) = Drehung des oberen Kreises, rot(U) = Drehung des unteren Kreises und rot(A) = Drehung des Außenkreises bezeichnet wurden. Man erhält drei neue Belegungen und verfährt mit diesen analog. Man macht das solange, bis keine neuen Belegungen mehr entstehen. Die auf diese Weise zu findende abgeschlossene Belegungsgruppe hat 120 Elemente. Da es aber insgesamt 720 Belegungen von 6 Plätzen mit 6 Steinen gibt, ist die Anzahl der Äquivalenzklassen von Belegungen auf diesem Graphen 6.■
|
||||||||
| ▼ ▲ 10. Das Boss-Puzzle auf beliebigen elementaren Spielgraphen | ||||||||
|
Wie in Abschnitt 3 schon angedeutet, kann man die Verhältnisse bei allgemeinen Spielgraphen auf die Verhältnisse bei Achtergraphen zurückführen. Die dort vorgestellte Plausibilisierung lässt dies aber zunächst einfacher erscheinen, als es ist. Bei dem Reduktionsprozess eines Graphen durch die Belegung und Ausdemspielnehmens eines Bogens kann es nämlich zu einer Komplikation kommen, die dort nicht gezeigt wird.
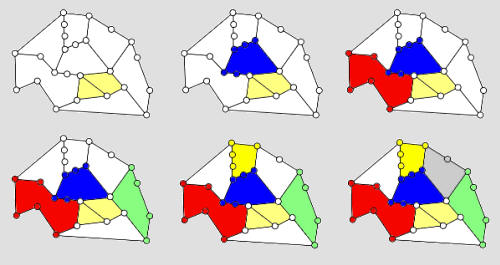
Abb. 22 Es liege also ein beliebiger elementarer Spielgraph vor (Bild 22, links). Wir wollen seine Ecken schrittweise mit den gewünschten Spielsteinen belegen. Dazu suchen wir uns einen enthaltenen Achtergraphen und belegen einen seiner Bögen mit den gewünschten Steinen (das geht immer, in Bild 22 sind das die geschwärzten Felder). Um das Erreichte im Folgenden nicht wieder zu zerstören, dürfen diese Steine nicht mehr bewegt werden. Damit scheiden alle Kanten aus dem Spielgraph aus, die zu Feldern dieses Bogens führen. Der daraus resultierende Spielgraph ist nun aber nicht mehr elementar, die Steine auf den nicht geschwärzten Feldern des ausgewählten Achtergraphen können nicht in den unteren Teil des Graphen transportiert werden und umgekehrt. Man findet in dem vorliegenden Graphen allerdings eine iterative Abbaureihenfolge, die bei einem Unterachtergraphen endet, der nur eine Äquivalenzklasse von Belegungen hat. Somit hat auch dieser Graph nur eine Äquivalenzklasse von Belegungen. Man steht nun vor dem Problem zu zeigen (oder zu widerlegen), dass es stets eine Abbaureihenfolge gibt, die bei einem vorher ausgewählten Achtergraphen endet. Bei der ersten Bearbeitung dieses Problemfelds in unserer Oberstufengruppe beließen wir es bei der Vermutung, dass dies stets möglich sei. Viele Jahre später thematisierten wir das Graphen-Boss-Puzzle in einer anderen Oberstufengruppe. Auch hier war es wieder eine gut zusammenarbeitende Gruppe von Mädchen, die sich sehr intensiv auch in ihrer Freizeit dieses Problems annahmen und zu der Thematik eine Arbeit bei „Jugend forscht“ einreichten. Ihre Beweisidee soll hier zum Schluss kurz skizziert werden. Sie benutzt einen besonderen „Kniff“, den man als Abbauen in der Aufbaureihenfolge charakterisieren kann. Wir reden im Folgenden von plättbaren elementaren Spielgraphen. Wir betrachten diese nun als Landkarten, deren Länder wir sukzessiv einfärben. Dabei färben wir die Ecken mit ein.
Abb. 23 Das zuerst eingefärbte Land ist der einklassige Achtergraph, auf den der Spielgraph letztlich reduziert wird. Dabei belegt man den farbigen Bogen des zuletzt hinzugekommenen Landes zuerst und schreitet dann weiter abwärts.
Endergebnis: Die Anzahl der Äquivalenzklassen von Belegungen auf zweifach zusammenhängenden Graphen ist also 1, 2 oder 6. Der Einsiedlergraph ist der einzige dieser Graphen mit 6 Äquivalenzklassen. Falls ein zweifach zusammenhängender Graph einen überschneidungsfreien Teilkreis mit ungerader Eckenzahl enthält (und es sich bei diesem Graphen nicht um den Einsiedlergraph handelt), gibt es genau eine Äquivalenzklasse, sonst 2.
|
||||||||
| ▼ ▲ 11. Literatur | ||||||||
|
Hier findet man eine Online-Ausgabe von Ahrens, W., "Mathematische Unterhaltungen und Spiele", Teubner, Leipzig 1901 Die oben wiedergegebenen Auszüge sind aus dieser Ausgabe.
|
||||||||
| ▲ Impressum | ||||||||
| Link zur Institutsseite: | Dr. Hartmut Rehlich, IDM Braunschweig, Bienroder Weg 97, 38106 Braunschweig | |||||||
|
Die übliche Bitte: Sollten dem Leser dieser Seiten Fehler in Orthographie, Sinn und Verstand auffallen, so bittet der Verfasser um Nachsicht und Nachricht und bittet auch darum, die Tücken der Technik (auf die auch andere hingewiesen haben) zur Entschuldigung ins Kalkül zu ziehen:
|
O unberachenbere
Schreibmischane,
--- Du tappst die
falschen Tisten, luber Bieb! von J. Guggenmoos |
|||||||