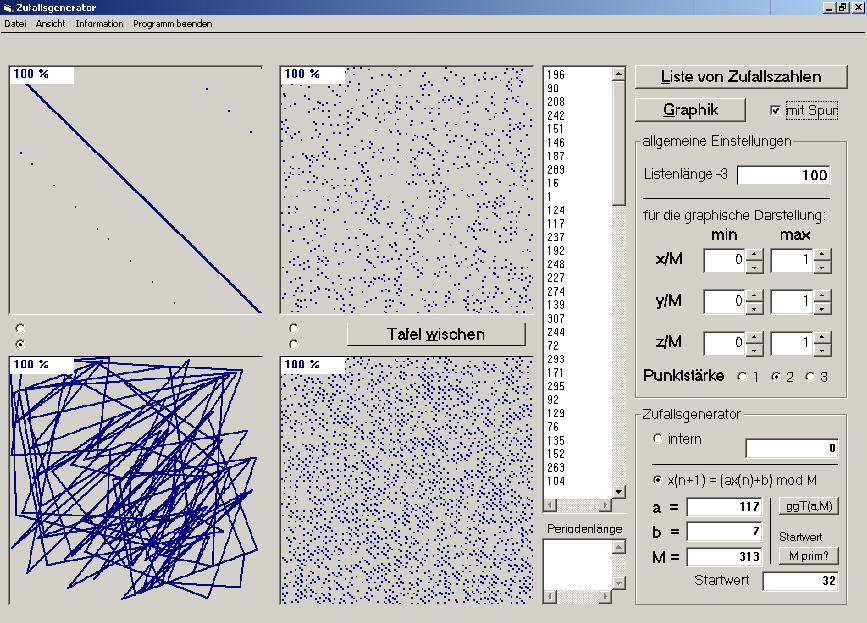
Die Programmierung verschiedener Zufallsgeneratoren ZG erzeugt Pseudo-Zufallszahlen. Man kann diese auf z. T. subtile geometrische Muster hin untersuchen und algebraische und zahlentheoretische Analysen zur Erklärung gewisser Muster durchführen.
Mit Hilfe des Programms kann man den internen ZG "unter die Lupe nehmen" und eigene Generatoren definieren und untersuchen.

|
Weit verbreitet sind lineare Kongruenzgeneratoren: x(n+1) = a*x(n) +b modulo M. Diese erzeugen Perioden, die bestenfalls die Länge M haben. Man kann diese Generatoren im Programm definieren und analysieren. Z. B. arbeitet der TI-59 mit a = 24298, b = 99991 und M = 199017 und hat eine maximale Periodenlänge. |
Man kann - durch die Betrachtung von Beispielen mit kleineren Zahlen - auf experimentellem Weg Hypothesen über das Verhalten verschiedener Zufallsgeneratoren aufstellen und so Anregungen für die "mathematische Denkarbeit" gewinnen.
Eine visuelle Analyse kann auch zur Entdeckung des Satzes von Marsaglia (1968) über diesen Generatortyp führen (bei geeigneter Deutung der Zufallszahlenfolge als Punktefolge im Raum findet man eine kleine Anzahl von Hyperebenen, auf denen alle Punke liegen).
Im Zusammenhang mit den vielfältigen möglichen Analysen können Primzahlen (Mersennsche und Fermatsche), Primitivwurzeln, kgV und ggT und weitere Begriffe aus der Teilbarkeitslehre - je nach Ausrichtung der Beschäftigung - wichtig werden.
Vor allem ist es jedoch besonders reizvoll den oft gar nicht zufällig aussehenden "Strickmustern" der Zufallszahlenreihen nachzuspüren.
download des Programms (644 KB)