Artikel als pdf-Datei (ausführlicher als hier)
Zwei Problemfelder um die Fibonaccifolge modulo n
1. Zu den Zyklenlängen der Fibonaccifolge modulo n
ein Problemfeld zum Weiterarbeiten
Ein einfacher Schubfachschluß beweist, daß die Fibonaccifolge modulo n für jedes n zyklisch ist. Aber wie lang sind die Zyklen? Eine Materialsammlung zur Mustererkennung führt schnell zu verschiedenen Hypothesen. Zu einigen werden Beweismöglichkeiten aufgezeigt, andere sind als Anregung für die Weiterarbeit in Fördergruppen oder Seminaren gedacht.
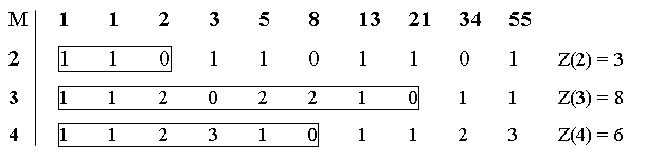
Betrachtet man die Fibonaccifolge 1, 1, 2, 3, 5, 8, 13, 21, 34 ..., so fällt das gerade-ungerade-Muster „uuguuguug...“ auf. Die Folge wird zyklisch mit der Zyklenlänge Z(2)=3. Die Tabelle zeigt die Zyklen auch für drei und vier.
Bild 1
Natürlich braucht man die Fibonaccifolge mit ihren großen Zahlen nicht, um die Folge modulo M hinzuschreiben, man startet einfach mit f0=1 und f1=1 und rechnet mit der Rekursion fn ≡ fn-1 + fn-2 modulo M. Daß die Folge für jedes M zyklisch wird, zeigt ein ganz einfacher Schubfachschluß: Es gibt nur M2 Zweierkombinationen bei M Restklassen, also müssen nach spätestens M2 Schritten wieder zwei Einsen hintereinanderstehen und alles beginnt von vorn.
Für M = 11 erhält man die Folge 1, 1, 2, 3, 5, 8, 2, 10, 1, 0, 1, 1,.. mit der Zyklenlänge 10. Das liegt beträchtlich unter der vom Schubfachschluß angezeigten Grenze 121. Die Tabelle zeigt eine Liste der Zyklenlängen bis n = 199. Primzahlen sind mit einem Sternchen markiert.
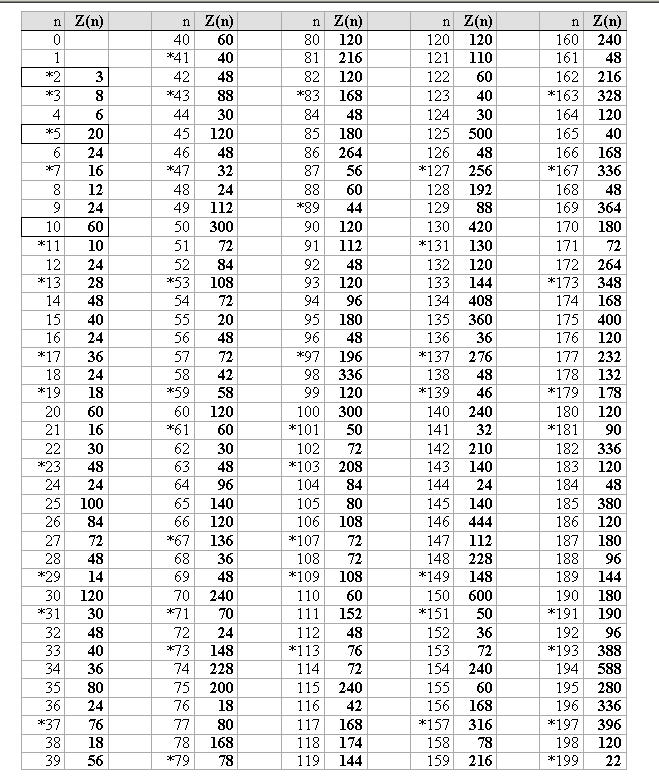
Bild 2
Die Tabelle zeigt ein auf den ersten Blick ein recht "sprunghaftes Verhalten" der Zyklenlängen. Bei näherem Hinsehen schälen sich aber schnell etliche mathematisch auffällige Muster (wie etwa gleich am Anfang (Z(2) = 3, Z(3) = 6, Z(6) = 18) heraus.
§1 Zusammengesetzte Zahlen
Einfach zu sehende und einfach zu beweisende allgemeingültige Muster:
■ Z(a∙b) = Z(a)∙(b), falls ggt(a, b) = ggt(Z(a), Z(b)) = 1 (Linearität bei "doppelter Teilerfremdheit")
■ Z(a∙b) = kgV(Z(a), Z(b)), falls ggt(a, b) = 1
■ Z(kgV(a, b)) = kgV(Z(a), Z(b))
Ein etwas komplexerer Zusammenhang kann vermutet werden:
■ Z(pa) = pa-1∙Z(p) für Primzahlen p
Wenn die Vermutung richtig ist, kann man die Zyklenlängen direkt berechnen:
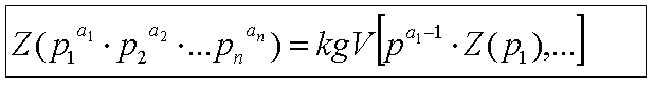
Man kann zeigen, daß die Vermutung dann richtig ist, wenn die Zyklenlänge modulo p2 größer ist, als die Zyklenlänge modulo p. Das ist für alle in Bild 2 tabellierten Werte gegeben. Die Frage, ob das aber für alle Primzahlen p so ist, könnte bis heute unbeantwortet sein (ich habe nichts dazu in der Literatur gefunden).
Ausführlicheres im pdf-Dokument
§2 Primzahlen
Unabhängig von der Richtigkeit der genannten Vermutung ist es aber natürlich sehr reizvoll, die Zyklenlängen der Fibonaccifolge für Primzahlmodule p zu untersuchen. Man kann auf elementare Weise einige Einsichten finden. (Einige grundlegende Einsichten in die Gruppen- und Körpertheorie sind dabei allerdings hilfreich).
Die Tabelle (Bild 2) zeigt vor allem zwei sofort ins Auge springende besondere Primzahlsorten:
Z(11) = 10, Z(19) = 18, Z(31 = 30), usw. Z(p) = p-1
Z(3) = 8, Z(7) = 16, Z(13) = 28), usw. Z(p) = 2(p+1)
Sieht man sich nun die Zyklenlängen für andere Primzahlmodule an, so merkt man schnell, daß die zugehörigen Zyklenlängen stets Teiler von p-1 oder von 2(p+1) sind und sich weitere auffällige "Untersorten" von Primzahlen finden lassen.
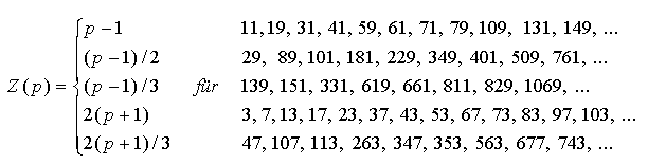
Bild 3
Primzahlen für die Z(p) ein Teiler von p-1 ist.
Die Zyklenlänge p-1 ist besonders auffällig. Schließlich ist p-1 die Anzahl der Elemente in der multiplikativen Restegruppe modulo p (die Reste primer Module bilden bekanntlich einen Körper). Dadurch wird der Gedanke nahegelegt, daß trotz der additiven Rekursionsformel der Fibonaccifolge multiplikative Strukturen eine entscheidende Rolle spielen. So kann man auf die Idee kommen, Folgen zu betrachten, die der Rekursionsgleichung der Fibonaccifolge genügen (sogenannte allgemeine Fibonaccifolgen) und gleichzeitig geometrische Folgen sind (so findet man ja auch eine explizite Darstellung der originalen Fibonaccifolge).
Die Betrachtung eines konkreten Beispiels ist, wie immer, sehr lehrreich. Wir wählen den Primzahlmodul 11 und betrachten eine solche Folge:
1 4 5 9 3 1 4
Diese Folge genügt der Rekursionsformel an+1 = an + an-1 und gleichzeitig an+1 = 4·an .
Eine zweite Folge dieser Art ist:
1 8 9 6 4 10 3 2 5 7 1 8
Es ist unmittelbar klar, daß alle geometrischen Folgen eine Zyklenlänge haben müssen, die Teiler von p-1 ist.
Die uns interessierende Folge, also die Fibonaccifolge
1 1 2 3 5 8 2 10 1 0 1 1
können wir aus diesen beiden Folgen linear kombinieren (wenn die ersten beiden Glieder stimmen, stimmt alles):
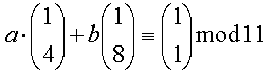Wir erhalten
a = 10 und b = 2 und so die
Fibonaccifolge als Summe zweier "übereinandergelegter" geometrischer Folgen:
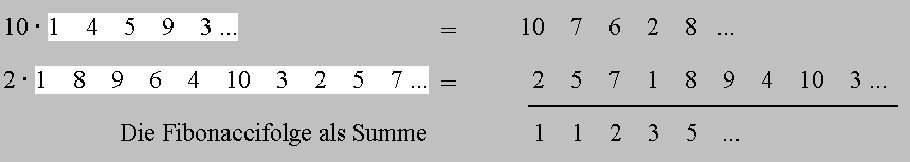
Dieses Beispiel ist in dem Sinne paradigmatisch, daß es aufzeigt, wie man für Primzahlmodule in denen zwei allgemeine Fibonaccifolgen existieren, die gleichzeitig geometrische Folgen sind, beweisen kann, daß die Zyklenlänge der Fibonaccifolge ein Teiler von p-1 ist. Im Beispiel ist die Zyklenlänge genau deshalb gleich p-1, also 10, weil eine der geometrischen allgemeinen Fibonaccifolgen, aus denen die Fibonaccifolge kombiniert wird, diese Zyklenlänge hat. Die Zyklenlänge der anderen geometrischen Folge ist nur 5.
Wenn man nun nur solche Primzahlmodule betrachtet, in denen zwei geometrische allgemeine Fibonaccifolgen existieren, muß man sich noch überlegen, ob das Gleichungssystem aus den beiden Kongruenzen zur Bestimmung der Gewichtungsfaktoren dann auch stets lösbar ist.
Darüberhinaus wünscht man sich auch ein einfaches Kriterium dafür, für welche Primzahlmodule zwei solcher allgemeinen Fibonaccifolgen existieren. Man findet, daß dies genau diejenigen sind, für die die Gleichung 1+x=x2 zwei verschiedene Lösungen hat und das sind genau diejenigen, für die man aus 5 die Wurzel ziehen kann. Letzteres kann man auch so ausdrücken: 5 muß quadratischer Rest modulo p sein.
Bild 3 legt die richtige Vermutung nahe, daß dies genau die Primzahlen sind, die kongruent +1 oder -1 modulo 5 sind. Die Begründung hierfür führt in die Theorie der quadratischen Reste.
Die zweite "Sorte" Primzahlen
Die Primzahlen p für die Z(p) ein Teiler von 2(p+1) ist, sind genau jene, für die es keine geometrischen Folgen gibt, die gleichzeitig allgemeine Fibonaccifolgen sind.
Um zu zeigen, daß für solche Primzahlmodule Z(p) stets ein Teiler von 2(p+1) ist, muß man etwas "tiefer" argumentieren. Man kann aber - noch immer recht elementar - mit dem erweiterten Zahlkörper aus p2 Elementen arbeiten.
Wir betrachten wieder ein "paradigmatisches Beispiel"
Im Restklassenkörper modulo 7 ist die Gleichung 1+x=x2 offenbar nicht lösbar (ausprobieren!). In den reellen Zahlen lautet die Lösung
.
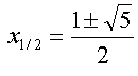Wir greifen nun zu einem "Trick": Wenn die Wurzel aus 5 modulo 7 nicht existiert, so konstruieren wir doch einen größeren Körper, der den Restklassenkörper modulo 7 enthält und in dem diese Wurzel existiert. Er besteht aus den Elementen
wobei a und b aus dem Restklassenkörper modulo 7
sind. Man rechnet leicht nach, daß diese "seltsamen Objekte" wieder einen Körper
bilden. Er hat p2 Elemente. Beim Multiplizieren zweier dieser
Elemente beachtet man, daß das Produkt
einfach den Rest 5 im
Restklassenkörper modulo 7 ergibt.
Nun haben wir einen Körper konstruiert, in dem es eben doch allgemeine Fibonaccifolgen gibt, die gleichzeitig geometrische Folgen sind. Somit können wir, wie oben, die Fibonaccifolge aus zwei verschiedenen solcher allgemeinen Fibonaccifolgen linear kombinieren und diese liegt dann natürlich ganz im zugrundeliegenden Körper.
Als Zyklenlängen kommen nun natürlich nur mögliche Zyklenlängen geometrischer Folgen im "Oberkörper" in Betracht. Die multiplikative Gruppe dieses Oberkörpers hat aber p2 - 1 Elemente. Dies ist (p-1)(p+1) und damit sind wir schon in die Nähe der Erkenntnis gerückt, daß die Zyklenlänge der Fibonaccifolge bezüglich dieser Primzahlen ein Teiler von 2(p+1) ist. Zum Beweis kann das Pascaldreieck modulo p und der kleine Fermatsche Satz herangezogen werden.
Ausführlicheres im pdf-Dokument
2. Zur Modellierung der optimalen Phyllotaxis
durch die Fibonaccifolge modulo n
ein Problemfeld zum Weiterarbeiten
Dem betrachtenden Auge zeigen sich Spiralstrukturen im Samenstand der Sonnenblume. Diese Spiralstrukturen fußen auf der Gestaltwahrnehmung bzw. Gestaltkonstruktion unseres Wahrnehmungsapparates. Ähnlich wie bei den bekannten „Kippbildern“, die bei längerer Betrachtung zwei verschiedene Gestalten zeigen, sehen wir auch hier verschiedene Spiralstrukturen. Im Bild der Sonnenblume sind zwei Scharen hervorgehoben. Die eine Schar hat 55 Spiralarme, die andere Schar hat 89 Spiralarme. Dies sind aufeinanderfolgende Fibonaccizahlen.
Die Computergraphik fußt auf einem einfachen rekursiven mathematischen Wachstumsmodell, welches aus der Analyse realer Pflanzen gewonnen wurde. Der Algorithmus funktioniert folgendermaßen:
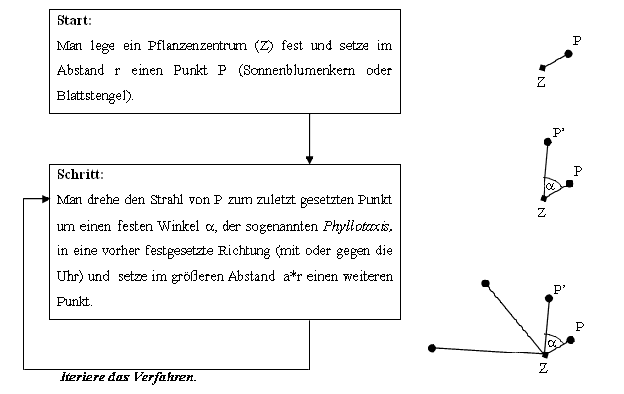
Je nach der Wahl des Streckungsfaktors a und der Phyllotaxis a erhält man verschiedene Ergebnisse. Die folgende Tabelle gibt die Phyllotaxis für einige Pflanzen an (in Anteilen vom Vollwinkel):
Ulme 1/2 Buche 2/3 Eiche 3/5 Pappel 5/8 Weide 8/13 Sonnenblume f
Wie man sieht, treten auch hier wieder die Fibonaccizahlen auf. Die Phyllotaxis der Sonnenblume ist in der Tat die Kleine-Goldene-Schnitt-Zahl (bei realen Sonnenblumen natürlich mit kleinen Abweichungen) und dies führt zu der Präsenz der Fibonaccizahlen bei der Anzahl der Spiralarme. Die Sonnenblume enthält den Goldenen Schnitt somit gleich auf zwei Arten. Mit dem folgenden Simulationsprogramm kann man sich für beliebige Phyllotaxiswinkel die entstehenden Strukturen anschauen. Es gibt viele Einstellmöglichkeiten (Radiuszunahme, Punktgröße etc) und man kann das Bild dynamisch laufen lassen und die Veränderungen betrachten.
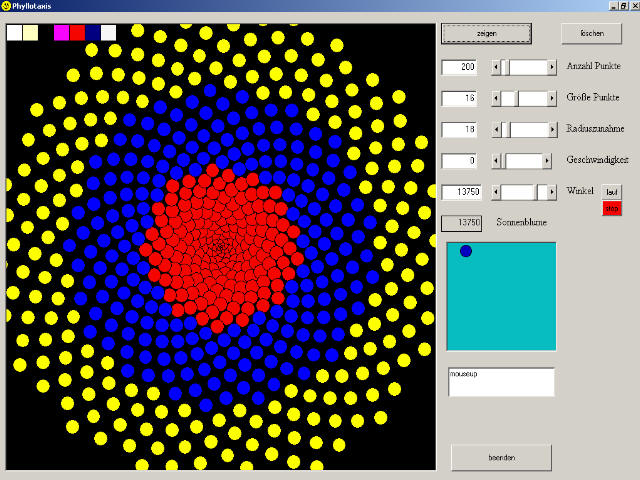
Angeregt durch die Feststellung, daß die Phyllotaxis der Sonnenblume der Goldene Winkel sei - also 360°/F, ungefähr 222,5°, das entspricht 137,5° in der Gegenrichtung- (man liest bei verschiedenen Autoren, daß damit eine gute Raumnutzung einhergehe) kann man auf die Idee kommen, den folgenden zyklischen Auffüllprozeß zu betrachten:
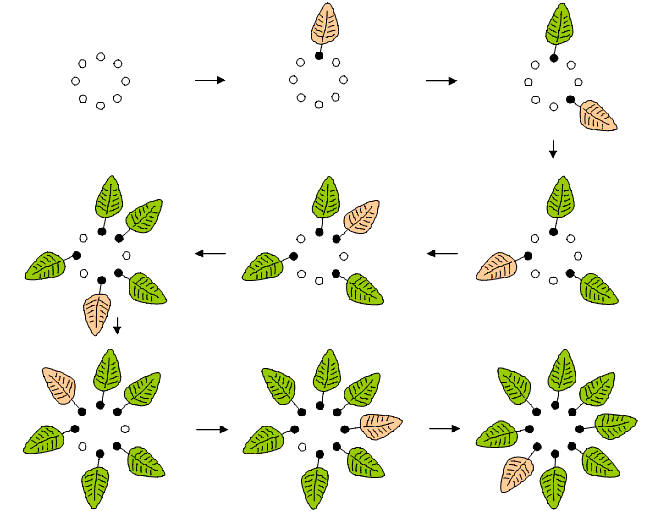
Man ordnet eine gewisse Anzahl N von freien Plätzen zyklisch an und füllt diese dann – stets um dieselbe Schrittzahl k in eine Richtung weitergehend – zyklisch auf (man läßt dort ein Blatt oder einen Kern wachsen). Das Bild zeigt diesen Auffüllprozeß für N = 8 und k = 5, das jeweils neu hinzugekommene Blatt ist etwas heller dargestellt.
Bei dem dargestellten Prozeß ist die Phyllotaxis also 135° (bzw. 225° gegen den Uhrzeigersinn) und somit wird der Goldene Winkel schon ganz gut approximiert. Das ist natürlich eine unmittelbare Folge davon, daß die hier gewählten Parameter N = 8 und k = 5 Fibonaccizahlen sind. Welche biologischen Vorteile bzw. mathematischen Besonderheiten damit verbunden sein könnten, ist an diesem kleinen Zahlenbeispiel noch nicht zu sehen. Insbesondere bleibt es noch begrifflich unscharf, was eine gute Raumnutzung bedeuten könnte, bzw. wie man diese mathematisch modellieren kann (es gibt sicher mehrere Möglichkeiten). Betrachten wir den Auffüllprozeß noch einmal bei einer Phyllotaxis von 45°:
Der Auffüllprozeß für N = 8 und k = 1:
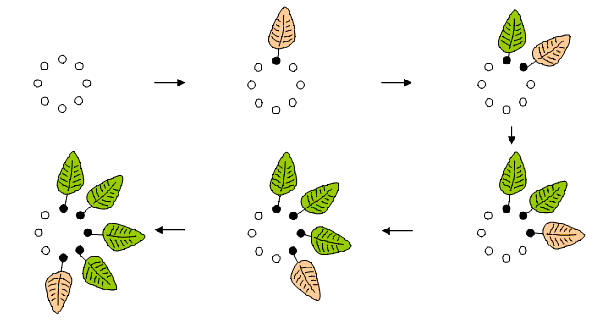
Die Zwischenstadien zeigen gegenüber dem vorigen Prozeß unharmonisch wirkende unausgewogene Zustände, die Blätter sind aufeinandergeballt, es sieht nicht nach guter Raumnutzung aus. Wir betrachten nun noch zwei weitere Auffüllprozesse und zwar für N = 13 und k = 5 bzw. k = 4. Die dekorativen Blätter werden im Folgenden weggelassen. Im Kreisinneren wird der mimimal vorkommende Abstand zwischen den bis zu diesem Stadium besetzten Plätzen notiert.
N = 13, k = 5
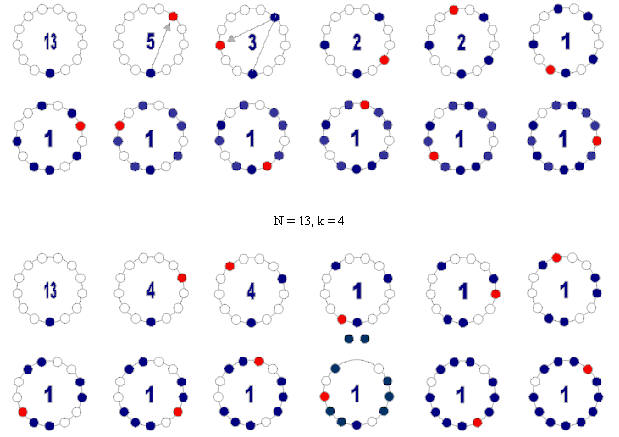
Schon an diesem kleinen Beispiel fallen mindestens zwei interessante Strukturen ins Auge. Wir vergleichen die Folgen der minimal vorkommenden Abstände A(i) bis zur Besetzung des i-ten Platzes:
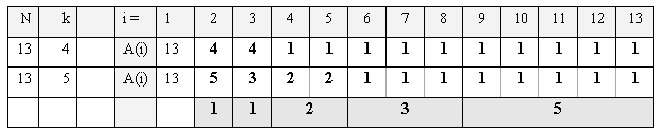
Beobachtung 1:
Betrachtet man die Folge der A(i) für N = 13 und k = 5 für sich allein, so fällt zunächst auf, daß alle Folgenglieder Fibonaccizahlen sind und zwar lückenlos absteigend ab F = 5.
Darüberhinaus ist die Häufigkeit des Auftretens der Fibonaccizahlen selbst wieder eine Fibonaccizahl.
Beobachtung 2:
Die Platznutzung ist für k = 5 in einer bestimmten Weise besser als für k = 4. Ab i = 4 ist der minimal vorkommende Abstand A(i) für k = 5 stets größer oder gleich als der minimal vorkommende Abstand A(i) für k = 4.
Bemerkungen:
Beobachtung 2 führt auf den Anlaß der Beschäftigung mit diesem Thema zurück. Denkt man nämlich an das Wachstum von Pflanzenteilen (Sonnenblumenkerne), so paßt die Idee einer guten Platznutzung ja durchaus zur Annahme, daß Selektionsprozesse für die Entwicklung der Phyllotaxis einer Pflanzensorte eine Rolle spielen und man aus diesem Grunde den Goldenen Winkel bei der Sonnenblume findet. Bei der Modellierung, was denn eine gute Raumnutzung sei, hat man aber natürlich zunächst viele Möglichkeiten. Ein erster Ansatz könnte darin bestehen, zu fordern, daß der jeweils neu hinzukommende Kern in der größten noch vorhandenen Lücke wächst. Daß dieser Modellansatz aber nicht auf den Goldenen Winkel führt, erkennt man an dem Eingangsbeispiel für N = 8 und k = 1: Der neu besetzte Platz liegt für k = 1 ganz offensichtlich immer in der größten noch vorhandenen Lücke, aber eben am Rand, also in direkter Nachbarschaft des vordem hinzugekommenen Kerns. Aus Beobachtung 2 dagegen könnte ein 1. Modell für „gute Platznutzung“ in diesem diskreten Wachstumsmodell abgehoben werden: Eine Phyllotaxis a ist besser als eine Phyllotaxis b, falls es ein i gibt, ab dem der Minimalabstand der Blätter A(i) für a stets kleiner oder gleich dem Minimalabstand der Blätter A(i) für b ist. Alternativ könnte man auch fragen wann das erste Mal ein Platz in direkter Nachbarschaft zu einem schon besetzten Platz besetzt wird und die Phyllotaxis als besser bezeichnen, bei der dies später geschieht (2. Modell).
An dieser Stelle des Bearbeitungsprozesses entsteht Bedarf nach einer größeren Grundlage von Beispielen zur Struktursuche bzw. zur psychologischen Absicherung erster Hypothesen. Daß Beobachtung 1 „kein Zufall sein kann“ (zu schön falsch zu sein), wird – falls man über diese Einsicht verfügt – heuristisch durch den Umstand gestützt, daß die Summe von Fibonaccizahlen F(i) bis zu einer bestimmten Stelle n um eins kleiner als die übernächste Fibonaccizahl F(n+2) ist.
Zur weiteren Erkundung des Problemfeldes kann ein zu diesem Zweck produziertes Computerprogramm (man sieht hier einen Screenshot) genutzt werden.
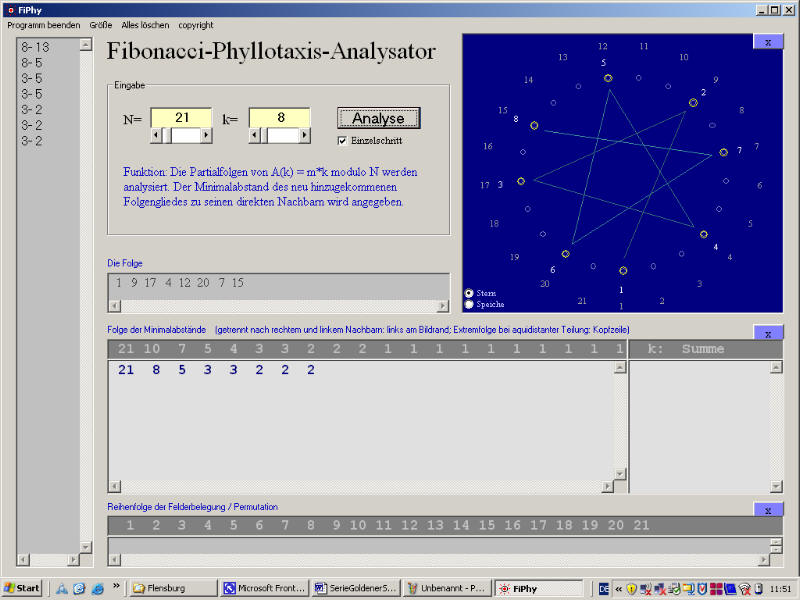
Bild: Zwischenstadium im Auffüllprozeß, bei dem 21 kreisförmig angeordnete Plätze zyklisch belegt werden. Die Folge der Minimalabstände ist 21, 8, 5, 3, 2, 2, 2,...