
1 + 2 = 3
4 + 5 + 6 = 7 + 8
9 + 10 + 11 + 12 = 13 + 14 + 15

Halbierbare Sequenzen -
ein Problemfeld aus der Elementarmathematik
zum entdeckenden Lernen
von Hartmut Rehlich
FSU Jena
Hinweis: Diese Seite enthält einige Computerprogramme zum Herunterladen. Diese können nach Belieben im Unterricht oder für eigene Untersuchungen eingesetzt werden.
Inhalt
•
•
a) in geometrischer Repräsentation
b) in arithmetischer Repräsentation
c) in algebraischer Repräsentation
•
•
a) links k Zahlen mehr als rechts
•
Eine offene Frage zum Weiterdenken: Gibt es drittelbare Sequenzen?
Weitere Problemfelder und Computerprogramme findet man hier
Zur Vorstellung des Problemfelds wird zunächst ein Arbeitsblatt wiedergegeben, das der Autor im "normalen Schulunterricht" in einem Hamburger Gymnasium in mehreren 11. Klassen eingesetzt hat.
Daneben haben wir in dem Problemfeld mit mehreren Gruppen innerhalb der Förderkurse für mathematisch besonders befähigte Schüler (im sog. Hamburger Modell) gearbeitet.

Die "Keimzelle" des Problemfelds ist die schöne Rechnung 1 + 2 = 3. Sie läßt sich in viele Richtungen verallgemeinern. Sucht man z.B. weitere Sequenzen aufeinanderfolgender natürlicher Zahlen, die in zwei summengleiche Teile gespalten werden können, bei denen links ein Summand mehr steht als rechts, so findet man schnell durch Probieren:
![]()
Die Augenscheinlichkeit der zu erkennenden Struktur läßt es berechtigt erscheinen, die vorangegangene Zeile mit "usw." abzuschließen. Die ersten Sequenzen passen "nahtlos" aneinander, und man vermutet (schnell und richtig), daß es so bleibt.
|
Sequenzen dieser Art werden im folgenden als "halbierbare Sequenzen" bezeichnet |
Um einen Überblick über den Beziehungsreichtum des Materials zu geben, werden einige Zusammenhänge im Problemfeld und mögliche Herangehensweisen dargestellt. Dabei wird vor allem auf didaktisch günstige Konstellationen aufmerksam gemacht. Es geht nicht darum, hier einen "linearen Weg" durch das Problemfeld aufzuzeigen. Vielmehr soll deutlich werden, daß Schüler entsprechend ihrer Fähigkeitsprofile verschiedene passende und Erfolg versprechende Betätigungsmöglichkeiten finden können. Diese sind u.a.
Material organisieren (mehr oder minder globale Übersichten mit leicht zu findenden Lösungen erstellen)
Muster im Material suchen
verschiedene Repräsentationen entwickeln und in diesen arbeiten
Hypothesen formulieren und testen
Begründungen suchen
Teilergebnisse formulieren
Anschlußprobleme erfinden
Nach der Organisation von Material können weitere auffällige Muster entdeckt werden. Alle gefundenen Sequenzen beginnen bei einer Quadratzahl, und links neben dem Gleichheitszeichen stehen immer "Heteromeken", das sind Zahlen der Form n·(n+1). Ausschnitte der vorgegebenen Art ohne diese Eigenschaften sucht man vergeblich.
Dieser Umstand regt zur Hypothesenbildung an. Als "Kontrollexperiment" für die sich aufdrängende Hypothese, daß bei jeder Quadratzahl eine solche Sequenz beginnt, kann mit größeren Zahlen gearbeitet und z.B. geprüft werden, ob der Ausschnitt von 10000 bis 10200 auch auf diese Weise teilbar ist. Die Bestätigung läßt die Hypothese dann "psychologisch sicher" werden. Das kann zur Suche nach Begründungen anregen und zur Erarbeitung eines Beweises führen. In diesem Zusammenhang kann sich die Frage nach einer Summenformel stellen, man kommt aber auch ohne eine solche aus.
a) in geometrischer Repräsentation
Wir betrachten halbierbare Sequenzen, bei denen links eine Zahl mehr als rechts steht. Das folgende Bild lehnt sich an die bekannten figurierten Zahlen der alten Griechen an und zeigt eine grundlegende Einsicht in die Struktur halbierbarer Sequenzen.
Beispiel: 9 + 10 + 11 + 12 = 13 + 14 + 15
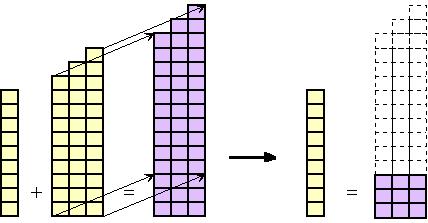
Allgemein: Der linke Abschnitt ist um 1 breiter als der rechte. Man kann daher stets einen Teil des linken Treppenabschnitt wie skizziert in Gedanken auf den rechten schieben und sieht, daß der Überhang offensichtlich immer ein Quadrat ist. Dieses muß durch den Vorspann kompensiert werden. Folglich muß die Startzahl eine Quadratzahl sein..
b) in arithmetischer Repräsentation
Das linke Subtraktionsmuster zeigt ebenso wie die obige geometrische Repräsentation, daß jede halbierbare Sequenz von einem Abschnitt angeführt wird, deren Summe eine Quadratzahl sein muß.
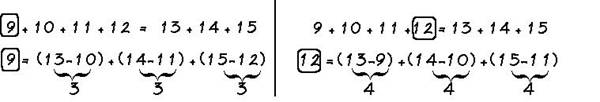
Das rechte Subtraktionsmuster bezieht sich auf die Heteromeken links vom Gleichheitszeichen. Auch für dieses Muster kann eine geometrische Darstellung gefunden werden.
c) in algebraischer Repräsentation
Alle Umformungen sind Äquivalenzumformungen und man sieht sofort, daß genau bei den Quadratzahlen derartige Sequenzen beginnen.
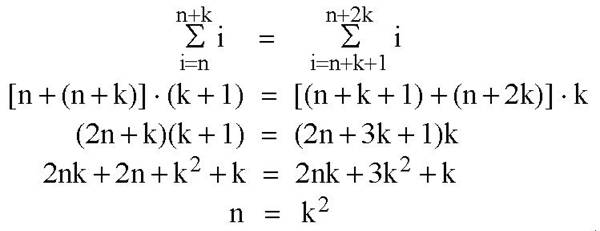
Abgesehen davon, daß Schülern zur algebraischen Lösung eventuell die nötige Routine fehlt, werden "ökonomisch optimierte" Darstellungen auch bei originärer mathematischer Arbeit von Fachleuten oft erst am Ende eines Theoriebildungsprozesses entwickelt.
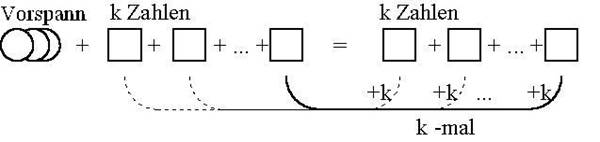
!
|
Innerhalb eines solchen Prozesses kann formal perfektes Arbeiten sogar den Blick auf weitere Zusammenhänge verstellen. Z.B. leistet die abgebildete formal weniger perfekte, eher ikonische Darstellung viel mehr (!) als die formelhafte Bearbeitung. Sie ist auch ohne große algebraische Umformungsfertigkeiten zu verstehen und sie ist unter heuristischen Gesichtspunkten sogar wesentlich besser. Sie zeigt nämlich den "eigentlichen Grund" für das Auftreten der Quadratzahlen, da - hinter der Startzahl - k-mal die Differenz k vorkommt. Darüber hinaus wird auch sofort erkennbar, daß es gar keine Rolle spielt, ob links eine, zwei oder drei Zahlen mehr als rechts stehen. Die Darstellung führt also zwanglos zu einer Verallgemeinerung der Einsicht: Die Summe des "Vorspanns" muß immer eine Quadratzahl sein, ganz gleich, wie viele Zahlen den "Vorspann" bilden. |
a) links k Zahlen mehr als rechts
Bei der Suche nach Beispielen kann man schnell und unbeabsichtigt auch solche finden, bei denen links zwei Zahlen mehr als rechts stehen. Bei der (nicht selbstverständlichen) Hinzunahme der Null findet man schnell Ergebnisse:
0+1 +2 = 3
4+5 + 6+ 7 +8 = 9 + 10 +11
12+13 + 14 + 15 + 16 +17 +18 = 19 + 20 +21 +22 +23
Von diesem Erfolg ermutigt, kann weiteres Material organisiert werden. Die sich herauskristallisierenden möglichen "Interpunktionsmuster" der Folge der natürlichen Zahlen sind ästhetisch reizvoll (sie "parkettieren den Zahlenstrahl") und können den Wunsch nach tieferer Einsicht auslösen.
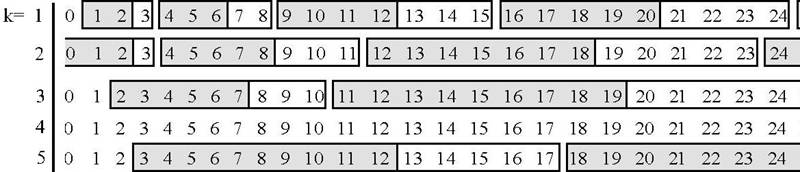
Die Zeile für k=4 bleibt leer!
In der vierten Zeile von oben sollten Sequenzen stehen, bei denen links vier Zahlen mehr als rechts stehen. Es wurde nicht vergessen, diese einzutragen, sondern es gibt keine Lösungen. Bei der Arbeit im Problemfeld kann das erfolglose Suchen solcher Sequenzen Verwunderung auslösen, denn vorher "lief alles sehr glatt". Im Beispielmaterial kann man auch noch entdecken, daß bei allen Sequenzen stets die Summe der ersten k Zahlen eine Quadratzahl ist. Daß man keine derartigen Ausschnitte findet, bei denen links vier Zahlen mehr als rechts stehen, kann zu der richtigen Vermutung leiten, daß die Summe von vier aufeinander folgenden Zahlen niemals eine Quadratzahl ist. Dadurch kann die Arbeit an der zahlentheoretischen Fragestellung, für welche Anzahl von Summanden dies überhaupt möglich ist, angeregt werden.
|
Die Summe von k aufeinanderfolgenden Zahlen kann genau dann eine Quadratzahl sein, wenn k - in seine Primfaktoren zerlegt - eine ungerade Anzahl von 2en enthält. |
Die Suche nach halbierbaren Sequenzen ist also nichts anderes, als die Suche nach Abschnitten in der Folge der natürlichen Zahlen, deren Summe eine Quadratzahl ist.
Wie das folgende Beispiel für k=8 zeigt, kann es für größere k sogar "mehrlagige Überdeckungen" geben:
| 4 + 11 = | 15 | 100 + 215 = | 315 | ||
| -3 -2 -1 0 1 2 3 4 5 6 | 7 8 | 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | 27 28 29 30 31 32 33 34 35 36 |
| 36 + 69 = | 105 | 196 + 497 = | 693 | ||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 15 16 17 18 19 20 | 21 22 23 24 25 26 27 28 29 30 31 ... 42 | 43 + 44 + 45 + ... 56 |
Wie man sieht, "parkettieren" die halbierbaren Sequenzen bei denen links 8 Zahlen mehr als rechts stehen (diese 8 Zahlen und ihre Summen sind jeweils weiß hervorgehoben) den Zahlenstrahl gleich doppelt. Jede halbierbare Sequenz bei der links 8 Zahlen mehr als rechts stehen gehört zu einer der beiden Serien.
Diese Einsicht kann man aus dem folgenden Satz, der Auskunft über sämtliche halbierbaren Sequenzen gibt, "extrahieren". Mit dem Satz sind natürlich nicht alle Strukturfragen für die man sich interessieren kann, explizit beantwortet (das ist bei keinem mathematischen Satz der Fall). Wenn man z.B. wissen möchte, ob es für irgendein k auch 37-lagige Überdeckungen gibt, kann man aber mit der im Satz verwendeten Analysemethode leicht weiterkommen.
|
Satz: Die Gesamtheit aller halbierbaren Sequenzen |
|
Stehen links k Zahlen mehr als rechts und k ist ungerade, so gibt es also eine mittlere Zahl M und die Summe des "Vorspanns" ist einfach k∙M und dies muß eine Quadratzahl sein.
k∙M = A2 Die Lösungen dieser diophantischen Gleichung beschreiben sämtliche halbierbaren S. mit ungeradem k.
Die Lösung dieser Gleichung ist trivial. Das kleinstmögliche M muß alle Primteiler die in ungerader Anzahl in k stecken genau einmal enthalten. Das kleinste M zu vorgegebenem k ist damit festgelegt und die weiteren erhält man einfach durch Multiplikation dieses minimalen M mit einer beliebigen Quadratzahl.
Beispiel 1: Links 5 Zahlen mehr als rechts: k = 5, 5∙M muß Quadratzahl sein, wähle also M = 5∙q2 mit beliebigem q. M = 5: 3 + 4 + 5 + 6 + 7 = 25 = 52 , 3+4+5+6+ 7 + 8+9+10+11+12 = 13+14+15+16+17 M = 5∙4 =20: 18 + 19 + 20 + 21 + 22 = 100 = 102 Beispiel 2: Links 27 Zahlen mehr als rechts: k = 27, 27∙M muß Quadratzahl sein, wähle also M = 3∙q2 mit beliebigem q.
Stehen links k Zahlen mehr als rechts und k ist gerade, so gibt es ein mittleres Zahlenpaar mit der ungeraden Summe M (die Summe zweier benachbarter natürlicher Zahlen ist immer ungerade) und die Summe des "Vorspanns" ist einfach k∙M/2.
k∙M/2 = A2 Die Lösungen dieser diophantischen Gleichung beschreiben sämtliche halbierbaren S. mit geradem k.
Da M ungerade ist muß k also eine ungerade Anzahl von 2en enthalten, sonst kann das Produkt k∙M/2 keine Quadratzahl sein. Die Lösungen dieser Gleichung sind ebenfalls offensichtlich.
|
|
Der Beweis ergibt sich aus dem vorher Gesagten. |
Es gibt viele weitere nahe liegende Sortierungen, z.B. nach Anfangsszahlen. Im letzten Fall findet man für die Anfangszahl 1 unendlich viele Lösungen und Verbindungen zur Approximation von der Wurzel aus 2. Dieser Zusammenhang kann "intuitiv visuell" gefunden werden, indem man die "Treppe" als Dreieck vereinfacht (für große Zahlen fällt die Stufigkeit immer weniger ins Gewicht).
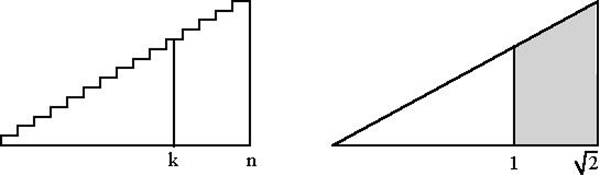
Man sieht, daß das Außendreieck zweimal die Größe des kleinen Dreiecks haben muß, wenn die Teilflächen gleich sein sollen. Das Außendreieck ist eine ähnliche Vergrößerung des kleinen Dreiecks und Flächenverdoppelung erhält man bei dem Streckungsfaktor n/k = Ö2.
Algebraisch:
Um alle Lösungen zu finden setzt man an:
n(n+1) = 2k(k+1) ↔ 4n(n+1) = 8k(k+1) ↔ (2n+1)2 - 1 = 2[(2k+1)2 - 1] ↔ A2 - 1 = 2[ B2 - 1] ↔ A2 = 2 B2 - 1
Man gelangt also zur Pelllschen Gleichung und damit auch zur Approximation der Wurzel aus 2.
Die Angabe aller Lösungen ist bei dieser Sortierung (nach Anfangszahlen) nicht so einfach, wie bei der Sortierung nach der Differenz der Anzahlen von Zahlen in den beiden Sequenzabschnitten. Man kann hier aber - ausgehend von den Lösungen der Pellschen Gleichung - eine Rekursion oder eine explizite Formel angeben.
Bei der Suche nach Lösungen der Pellschen Gleichung und ihren Verallgemeinerungen ist es unter heuristischen Gesichtspunkten günstig, sich einige Lösungen anzusehen (man entdeckt dann ein Rekursionsmuster und kann damit Beweise führen).
Das Computerprogramm "Sequenzen.exe" kann hier heruntergeladen und zur Organisation von Material und zur Mustersuche eingesetzt werden.
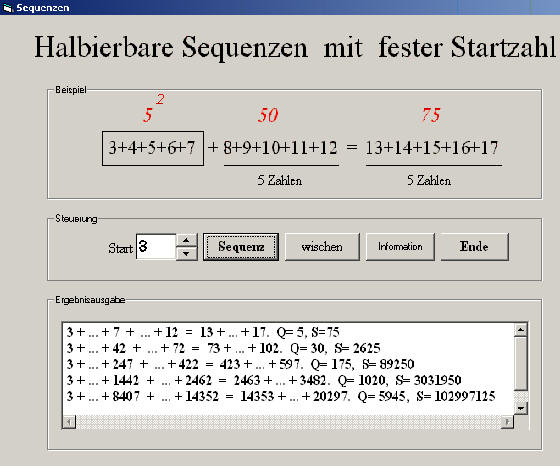
Ein anderer "Verallgemeinerungsweg", bei dem man die Folge der natürlichen Zahlen durch eine andere Folge, z.B. durch die Folge der Quadratzahlen ersetzt, kann durch die als Erfolg versprechend erlebte Strategie "spiele mit verschiedenen Zusammenfassungen" auch mit guten Aussichten bearbeitet werden:
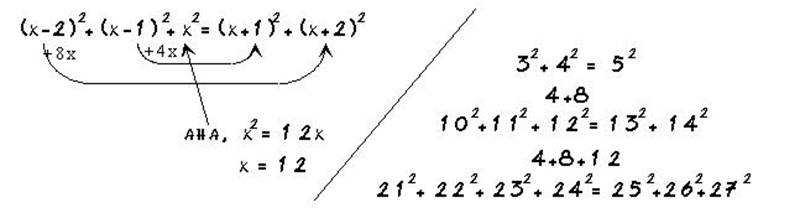
Das einfache pythagoreische Tripel 3,4,5 kann also als Anfang einer unendlichen Serie mit speziellen Eigenschaften aufgefaßt werden.
|
Das Spektrum verwandter Anschlußprobleme ist breit. Als weitere zugrundeliegende Folgen bieten sich die Folge der Stammbrüche, der Kuben und Ähnliches an. |
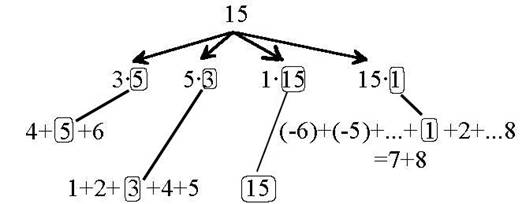
Man kann den Fokus aber auch darauf legen, daß die betrachteten Sequenzen zwei verschiedene Summendarstellungen aus aufeinander folgenden natürlichen Zahlen geben: 4+5+6 = 15 und 7+8 = 15. Dann liegt es nahe zu fragen, ob es weitere derartige Darstellungen für die 15 gibt. Man findet 1+2+3+4+5 = 15 und als trivialen Sonderfall auch 15 = 15. Dieses und weitere Beispiele können zur Begriffsbildung anregen. Bezeichnet man Zahlen, die auf genau k Arten als Summe aufeinander folgender natürlicher Zahlen dargestellt werden können, als "k-fach sequenzierbar", so lassen sich die folgenden Fragen stellen:
Gibt es für jedes k eine k-fach sequenzierbare Zahl?
Wie kann man für eine vorgelegte Zahl n ihr zugehöriges k berechnen?
n(k) sei die kleinste natürliche Zahl die k-fach sequenzierbar ist. Was kann man über die Folge der n(k) aussagen?
Um deutlich zu machen, daß es auch zur Bearbeitung dieses Anschlußproblems zunächst keines "Formelapparates" bedarf, wird - ohne weiteren Kommentar - dargestellt, wie man für die Summe S = 15 sämtliche möglichen Summationen der gesuchten Gestalt systematisch finden kann (die Methode kann ausgebaut und verallgemeinert werden):
Das Computerprogramm "Sequenzierer.exe" kann hier heruntergeladen und zur Organisation von Material und zur Mustersuche eingesetzt werden.
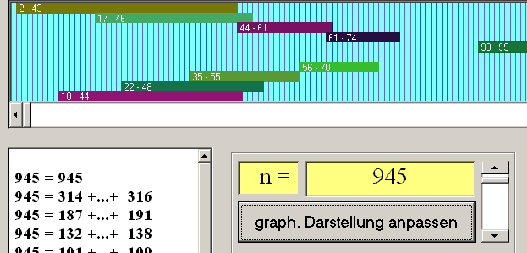
Teilansicht der Programmoberfläche
|
Man erkennt, daß 4 (der insgesamt 16 verschiedenen) Sequenzdarstellungen von 945 zwei halbierbare Sequenzen bilden ( 35 +... 55 = 56 +... 70 und 2 + ... 43 = 44 + ... 61). Beim "Herumspielen" kann man auf die Idee kommen, nach drei aufeinanderfolgenden summengleichen Abschnitten der natürlichen Zahlen zu suchen. |
Die aufgeführten Beispiele sollen verdeutlichen, daß - wie bei jeder mathematischen Theoriebildung - immer wieder neue Begriffsbildungen und Anschlußfragen entstehen können. Um das ursprüngliche Problemfeld kann ein beziehungsreiches Netz allgemeinerer und verwandter Strukturen wachsen. Die folgende Grafik gibt einen Überblick über verschiedene Dimensionen der Verallgemeinerungspfade des Ausgangsproblems.
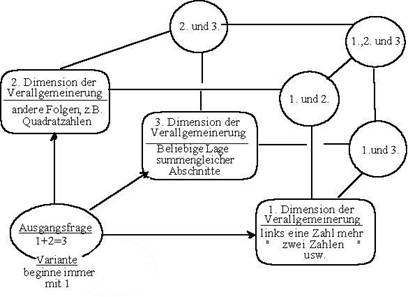
Mit dem bisher Gesagten sind die bei der Arbeit im Problemfeld zu entdeckenden Fragen und Strukturen natürlich keinesfalls erschöpfend beschrieben. Es folgen einige Anregungen für weitere Untersuchungen.
Die verwendeten Bezeichnungen werden an einem Beispiel erläutert:
"Halbierbare (r,s)-Sequenz", hier eine (7, 5)-Sequenz: 12+13 + 14 + 15 + 16 +17 +18 = 19 + 20 +21 +22 +23
Mit r wird also die Anzahl der Zahlen links vom Gleichheitszeichen bezeichnet, mit s die Anzahl der Zahlen rechts vom Gleichheitszeichen. Die "Startzahl" ist 12.
Für welche Verhältnisse r/s existieren halbierbare (r,s)-Sequenzen?
Man bestimme alle halbierbaren (r,s)-Sequenzen mit demselben Verhältnis r/s.
(Schwieriger:) Man betrachte alle halbierbaren (r,s)-Sequenzen mit konstanter Differenz r-s. Man beweise: jede natürliche Zahl ab einer Stelle N kommt in gleichvielen dieser Sequenzen vor.
Man lege nun die Folge der ungeraden Zahlen zu Grunde und suche hier nach analogen Strukturen.