Halbierbare Sequenzen -
ein Problemfeld aus der Elementarmathematik
zum entdeckenden Lernen
von Hartmut Rehlich, FSU Jena
zur Anschlußfrage:
Gibt es in arithmetischen Folgen drittelbare Sequenzen?
Die Antwort auf diese Frage ist "nein"
(Euler führte als erster einen Beweis, allerdings für eine Aussage, deren Äquivalenz zu der hier aufgeworfenen Frage erst gesehen werden muss)
Eulers
Beweis und später auch von anderen geführte Beweise sind
nicht trivial. Wenn man Muße hat, kann man - vermutlich
aussichtslos - nach elementareren Beweisen suchen. Hier werden ein paar
Ideen vorgestellt und auch die Äquivalenz zum Satz "Es gibt keine
4 Quadratzahlen in arithmetischer Progression" bewiesen (es versteht
sich von selbst, dass unsere Grundmenge die natürlichen Zahlen
sind).
Hinweis: Diese Seite enthält zwei Computerprogramm zum Herunterladen. Diese können nach Belieben im Unterricht oder für eigene Untersuchungen eingesetzt werden.
Was suchen wir?
1. Die gesuchte Struktur:

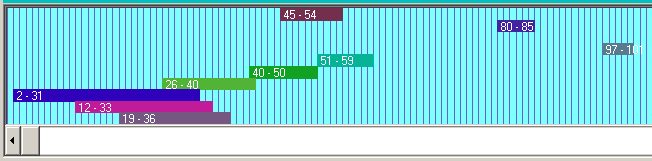
Die natürlichen Zahlen in den drei Abschnitten (durch die Sternchen angedeutet) ergeben stets dieselbe Summe.
Wir suchen also eine recht naheliegende Verallgemeinerung zu den halbierbaren Sequenzen (der Ausschnitt 4,5,6,7,8 aus der Folge der natürlichen Zahlen läßt sich durch ein Gleichheitszeichen in zwei summengleiche Teile zerschneiden: 4 + 5 + 6 = 7 + 8). Wir suchen nun nach Ausschnitten aus der Folge der natürlichen Zahlen, die man in drei summengleiche Abschnitte zerlegen kann.
2. Ein Äquivalent zur gesuchten Struktur (Beweis folgt):
Weiter unten wird gezeigt, daß eine solche unter 1. beschriebene Struktur genau dann existiert, wenn es eine viergliedrige arithmetische Progression aus Quadratzahlen gibt, d.h. die vier natürlichen Zahlen
x2 ♦ x2 + 1d ♦ x2 + 2d ♦ x2 + 3d
sollen Quadratzahlen sein.
Anmerkung: Dreigliedrige arithmetische Progressionen aus Quadratzahlen existieren (zwischen diesen und den halbierbaren Sequenzen gibt es eine Verbindung, diese wird weiter unten aufgezeigt) Dies ist z. B. eine dreigliedrige arithmetische Progression die nur aus Quadratzahlen besteht:
1 ♦ 1 + 24 = 25 ♦ 25 + 24 = 49
Viergliedrige arithmetische Progressionen aus Quadratzahlen gibt es allerdings nicht, das wurde schon von Leonhard Euler bewiesen.
1. Ansatz: Ein diophantisches Gleichungssystem
Erste Bedingung
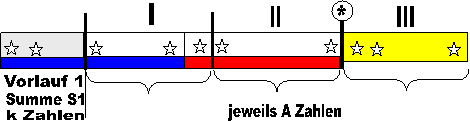
Wegen der kleineren Zahlen im roten und im blauen Abschnitt (als im gelben), enthalten diese jeweils mehr als A Zahlen (der rote Bereich A+x Zahlen) und man kann die Breite des gelben Streifens also dreimal abtragen. Übrig bleibt ein Vorlauf, dessen Summe 3A2 betragen muß. Das liegt daran, daß die Summe der Zahlen in Abschnitt II um A2 kleiner als die Summe der Zahlen in Abschnitt III und die Summe der Zahlen in Abschnitt I um 2A2 als die Summe der Zahlen in Abschnitt III ist. Da die Summe links von * aber doppelt so groß sein muß wie die Summe der Zahlen im gelben Abschnitt, müssen die fehlenden 3A2 durch den Vorlauf kompensiert werden.
Bedingung I: S1 = 3A2
Zweite Bedingung
Der blaue und der rote Abschnitt bilden zusammen eine halbierbare Sequenz. Auch diese hat einen Vorlauf 2, dessen Summe S2 eine Quadratzahl ist. Vorlauf 2 ist um 2x kürzer als Vorlauf 1 (enthält also k-2x Zahlen) und beginnt bei derselben Zahl wie Vorlauf 1.

Bedingung II: S2 = (A+x)2
Zusammenführung
Die Summe der k Zahlen in Vorlauf 1 ist S1 = k∙M , wobei M der Mittelwert dieser k Zahlen ist.
Für ungerades k ist M also eine ganze Zahl (eben die in der Mitte stehende), sonst die Hälfte einer ungeraden Zahl (steht z. B. ...5, 6.... in der Mitte, also 5,5).
Die Summe der k-2x Zahlen in Vorlauf 2 ist S2 = (k-2x)∙(M-x) (wieder Anzahl ∙ Mittelwert).
Damit erhält man die folgenden „Gesamtbedingungen“:
1. Fall: k sei ungerade
Es gibt genau dann drittelbare Sequenzen, wenn die beiden diophantischen Gleichungen
k∙M = 3A2 und (k-2x)∙(M-x) = (A+x)2 gleichzeitig erfüllbar sind.
Alle Variablen und alle Faktoren müssen natürliche Zahlen sein.
1. Fall: k sei gerade
Es gibt genau dann drittelbare Sequenzen, wenn die beiden diophantischen Gleichungen
k∙U = 6A2 und (k-2x)∙(U-2x) = 2(A+x)2 gleichzeitig erfüllbar sind.
Alle Variablen und alle Faktoren müssen natürliche Zahlen sein. U steht für eine ungerade natürliche Zahl.
Dieser Ansatz kann weiter verfolgt werden, dem Autor ist leider kein Beweis dafür, dass keine Lösung existiert, gelungen.
2. Ansatz: Arithmetische Progressionen aus Quadratzahlen (Äquivalenz zum Eulersatz)
Die folgenden Betrachtungen werden zwar an konkreten Beispielen veranschaulicht, sind jedoch allgemeingültig. Ihr Wert liegt darin, daß sie zeigen, daß es für die zu untersuchenden Zusammenhänge gar keinen Unterschied macht, ob man die Folge der natürlichen Zahlen oder irgendeine andere arithmetische Folge zugrundelegt. Nimmt man die ungeraden Zahlen, so sieht man die Äquivalenz der Aussagen mühelos. Legt man die Folge der natürlichen Zahlen zugrunde, so muss man etwas mit Umformungen spielen. Wir betrachten zuerst den einfacheren Fall und suchen also in der Folge 1, 3, 5, 7, 9, 11 nach halbierbaren Sequenzen.
|
Die Folge der ungeraden Zahlen |
||||||||||||||
| Bezeichnung | x | a | b | |||||||||||
| ↓ | ↓ | ↓ | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |||
| ↑ | ↑ | ↑ | ||||||||||||
| Summe bis x, a bzw. b | 12 | +24 | 52 | +24 | 72 | |||||||||
| Bedingung (allg.) |
b2 - a2 = a2 - x2 |
|||||||||||||
|
Die Suche nach halbierbaren Sequenzen in der Folge der ungeraden Zahlen ist also nichts anderes, als die Suche nach einer dreigliedrigen arithmetischen Progression in der Folge der Quadratzahlen. Zu der halbierbaren Sequenz 3+5+7+9 = 11+13 ist also die Progression 12 , 52 , 72 eindeutig zugeordnet. Für eine drittelbare Sequenz wären also eine vierte Quadratzahl zu suchen, die wieder denselben Abstand zur vorherigen Quadratzahl hat. Nun kommt das angekündigte Umformungsspiel, mit dessen Hilfe man einsieht, dass die Äquivalenz auch dann besteht, wenn man die Folge der natürlichen Zahlen zugrundelegt.
|
||||||||||||||
| Die Folge der natürlichen Zahlen | ||||||||||||||
| x | a | b | |||||||||||||||||
| ↓ | ↓ | ↓ | |||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||||||
| ↑ | ↑ | ↑ | |||||||||||||||||
| Summe bis x, a, bzw. b | 6 | +30 | 36 | +30 | 66 | ||||||||||||||
| Bedingung (allg.) |
b(b-1) - a(a-1) = a(a-1) - x(x-1) |
||||||||||||||||||
|
Transformation der Sequenz in die Folge der ungeraden Zahlen mit f(z) = 2z + 1 |
|||||||||||||||||||
| f(x) | f(a) | f(b) | |||||||||||||||||
| ↓ | ↓ | ↓ | |||||||||||||||||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| ... | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| ↑ | ↑ | ↑ | |||||||||||||||||
| 72 |
+240 |
172 |
+240 |
232 | |||||||||||||||
|
Die Suche nach halbierbaren Sequenzen in der Folge der natürlichen Zahlen ist also ebenfalls nichts anderes, als die Suche nach einer dreigliedrigen arithmetischen Progression in der Folge der Quadratzahlen.
|
|||||||||||||||||||
Falls die Allgemeingültigkeit des Beispiels nicht gesehen wird:
Die hier exemplarisch vorgenommene Transformation fußt darauf, daß die Summenformel für die natürlichen Zahlen eine quadratische Funktion ist und man diese in die Scheitelpunktsform transformieren kann.
Daher ist es gar kein Unterschied, ob man b2 - a2 = a2 - x2 oder D(b) - D(a) = D(a) - D(x) ↔ b(b-1) - a(a-1) = a(a-1) - x(x-1) fordert. Letzteres kann nämlich (nach Multiplikation mit 4) in (2b-1)2 -1 - [(2a-1)2 -1] = (2a-1)2 -1 - [(2x-1)2 -1] überführt werden und hier heben die quadratischen Ergänzungen einander auf. Man kann sich überlegen, daß das stets auch bei anderen zugrundeliegenden arithmetischen Folgen der Fall ist, da diese ja stets quadratische Summenformeln haben, die alle in die Scheitelpunktform transformiert werden können.
|
gesucht ist also eine arithmetische Progression x2 ♦ x2 + 1d ♦ x2 + 2d ♦ x2 + 3d aus 4 Quadratzahlen
|
Quadratische Reste; Teilbarkeitsbetrachtungen:
Bei der folgenden Betrachtung modulo 5 sind alle quadratischen Reste rot gefärbt. Wenn es eine arithmetische Progression aus vier Quadratzahlen gäbe, wäre diese natürlich auch modulo 5 eine solche Progression.
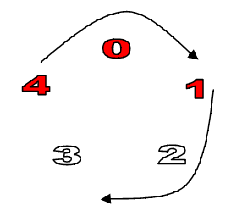
Bild: 5 muß ein Teiler von d sein
Diese Progression würde sich in der Grafik als ein Rundlauf mit konstanter Schrittlänge darstellen, der nur auf rot markierte Zahlen trifft. Man sieht schnell, daß das nicht möglich ist, es sein denn, man wählt die Schrittlänge d ≡ 0 modulo 5 und tritt quasi auf der Stelle (im Beispiel ist zu sehen, daß für d = 2 modulo 5 schon der zweite Schritt keinen quadratischen Rest trifft, für d=1 liegen die quadratischen Reste 4, 0 und 1 in arithmetischer Progression, aber 2 ist dann kein quadratischer Rest mehr.):
Man kann analog ebenso zeigen, daß 3, 4, 7 und 11 Teiler von d sein müssen. Zur Illustration sind für 11 noch einmal die quadratischen Reste gelb markiert. Man sieht hier durch Probieren, daß es unter diesen zwar arithmetische Progressionen aus drei Gliedern gibt (z. B. 3-4-5, 9-1-4 und 1-5-9), aber keine arithmetische Progression der Länge 4, es sein denn, man „tritt wieder auf der Stelle“ indem man d=11 wählt.
![]()
Für die Teiler 3, 4, 7 kann man ganz analog argumentieren.
Ergebnis dieser Betrachtung:
Wenn es also überhaupt eine Lösung gibt, muß 3∙4∙5∙7∙11= 4620 ein Teiler von d sein.
Alle Module, für die man analog argumentieren kann, scheinen aus diesen 5 Zahlen multiplikativ zusammengesetzt zu sein. Insbesondere ist es mir nicht gelungen, einen größeren Modul als 4620 zu finden, in dem es keine viergliedrige arithmetische Progression von Quadratzahlen gibt.
Das hat eine Computeranalyse ergeben und dies ist höchst bedauerlich. Fände man nämlich eine unendliche Folge von Modulen in denen es bis auf die Schrittlänge d=0 keine Lösung gibt, wäre damit nämlich die Nichtexistenz drittelbarer Sequenzen bewiesen (dann müßten nämlich alle diese Module d teilen, was ja nicht möglich ist).
Da nun aber bekanntlich die Hälfte aller Reste (außer 0) bezüglich eines Primzahlmoduls quadratische Reste sind, wird es natürlich bei größeren Primzahlen auch immer "unwahrscheinlicher", daß diese so liegen, daß man keine arithmetische Progression der Länge 4 finden kann.
zurück zu
gesucht ist also eine arithmetische Progression
x2 ♦ x2 + 1d ♦ x2 + 2d ♦ x2 + 3d
aus 4 Quadratzahlen
Erwähnenswert ist auch noch, daß man ohne weiteres Beispiele für alle Kombinationen aus 3 Bedingungen (natürlich immer inklusive x2) finden kann, aber eben keine, für die alle Glieder der Progression Quadratzahlen sind.
|
|
d=24 |
d=8 |
d=528 |
|
x2 |
1 |
1 |
625 |
|
x2+d |
25 |
9 |
|
|
x2+2d |
49 |
|
1681 |
|
x2+3d |
|
25 |
2209 |
Die (vermutete) Nichtexistenz von Lösungen „hängt“ also an dem Zusammenspiel der 4 Forderungen.
Ein mit Hilfe "Pellscher Gleichungen" gewonnener Satz
(Transport des Problems in die Menge der verallgemeinerten Fibonaccifolgen)
Die Überlegung wird der Anschaulichkeit zuliebe an einem „paradigmatischen Beispiel“ erläutert (x=1). Man kann das aber sehr leicht verallgemeinern.
|
Satz Die Aussage: Die vier Zahlen x2 x2 + 1∙d x2 + 2∙d x2 + 3∙d können für festes x und d nicht alle Quadrate natürlicher Zahlen sein.
ist für x=1 genau dann richtig,
wenn die beiden rekursiv definierten Folgen a0 = a1= 1 und an+1 = 6an - an-1 für n>0 b0 = b1= 1 und bn+1 = 4bn - bn-1 für n>0
Für n>1 kein gemeinsames Folgenglied haben.
|
Bemerkung: Der Satz ist für jedes beliebige x richtig. Die Einschränkung x=1 in der Behauptung wurde nur gemacht um einen einfacheren Beweis führen zu können. Der Leser kann diesen selbst verallgemeinern. Der Sinn des Satzes liegt darin, daß er die Suche nach drittelbaren Sequenzen nun in den Bereich "verallgemeinerter Fibonacci-Folgen" trägt. Bei den hier zu untersuchenden Folgen wird analog zur Fibonacci-Folge das nächste Folgenglied jeweils aus seinen beiden Vorgängern linear kombiniert .
Beweis:
Falls es eine arithmetische Progression der gesuchten Form gäbe, wären also gleichzeitig die zwei unten gezeigten Dreiergruppen von Bedingungen I und II ganzzahlig erfüllbar. Man betrachtet nun alle Lösungstupel der beiden Teilprobleme und sucht nach einem gemeinsamen a. Beide Bedingungen sind gleichwertig mit je einer Pellschen Gleichung und deren Lösungen mit den entsprechenden bekannten Rekursionstypen sind im folgenden Kasten angegeben (die Herleitung fehlt hier also, das gängige Verfahren wird als bekannt vorausgesetzt). Die Rekursionen wurden dann jeweils allein für die Folgen der <a> zusammengefaßt, die zweite Variable wurde also "rausgeworfen".
|
I |
x2 = 1 |
k |
1 |
2 |
3 |
4 |
|
ak+1 = 3ak + 2bk |
|
|
a2 = 1 + 1∙d |
ak |
1 |
5 |
29 |
169 |
|
bk+1 = 4ak + 3bk |
|
|
b2 = 1 + 2∙d |
bk |
1 |
7 |
41 |
239 |
|
|
|
|
b2 = 2∙a2 - 1 |
B1 |
ak+1 = 6ak - ak-1 |
|
II |
x2 = 1 |
k |
1 |
2 |
3 |
4 |
|
ak+1 = 2ak + ck |
|
|
a2 = 1 + 1∙d |
ak |
1 |
3 |
11 |
41 |
|
ck+1 = 3ak + 2ck |
|
|
c2 = 1 + 3∙d |
bk |
1 |
5 |
19 |
71 |
|
|
|
|
c2 = 3∙a2 - 2 |
B2 |
ak+1 = 4ak - ak-1 |
Wenn die Bedingungen B1 und B2 gleichzeitig erfüllbar wären, müßte sich in beiden Fällen also "irgendwo das gleiche a vorfinden" (natürlich an verschiedenen Stellen, denn die erste Folge wächst ja sichtlich schneller). Wir haben so erhalten:
Genau dann wenn es in den beiden rekursiv definierten Folgen
a0=1. a1 = 1, a2 = 5, an+1 = 6an – an-1 für n >1
b0=1, b1 = 1, b2 = 3, bn+1 = 4bn – bn-1 für n >1
![]() ein
gemeinsames Glied gäbe, wären also beide Bedingungen gleichzeitig erfüllbar,
sonst nicht.
ein
gemeinsames Glied gäbe, wären also beide Bedingungen gleichzeitig erfüllbar,
sonst nicht.
Damit haben wir die Frage in den Bereich der verallgemeinerten Fibonaccifolgen getragen, aber auch hier keinen Beweis anzubieten.
Anmerkung: Man kann sich - mit denselben Methoden wie bei der Fibonacci-Folge - auch explizite Darstellungen für die einzelnen Folgenglieder beschaffen.
Eine "astronomische Abschätzung"
Der oben bewiesene Satz regt auch zu einer "experimentalmathematischen Exkursion" an. Man kann mit Hilfe einer Tabellenkalkulation oder eines kleinen Computerprogramms prüfen, ob man in einem gewissen Zahlbereich gleiche a's findet:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 1 | 5 | 29 | 169 | 985 | 5741 | 33461 | 195025 | 1136689 | 6625109 | 38613965 | 225058681 | 1311738121 | 7645370045 | 44560482149 |
| 1 | 1 | 3 | 19 | 111 | 647 | 3771 | 21979 | 128103 | 746639 | 4351731 | 25363747 | 147830751 | 861620759 | 5021893803 | 29269742059 |
Wie man sieht, stößt das aber sehr schnell an eine Grenze, die Folgen wachsen - ebenso wie die Fibonaccifolge - im Wesentlichen exponentiell und man verläßt daher schnell den Bereich, in dem Computer mit ganzen Zahlen rechnen.
Mit einem kleinen "Trick" bleiben die Folgenglieder aber klein: Man betrachtet die Folge nur hinsichtlich der Divisionsreste ihrer Folgenglieder. Man kommt so zu "Folgen modulo n". Die folgende Tabelle zeigt dieselben Folgen modulo 7:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 1 | 5 | 1 | 1 | 5 | 1 | 1 | 5 | 1 | 1 | 5 | 1 | 1 | 5 | 1 |
| 1 | 1 | 3 | 4 | 6 | 6 | 4 | 3 | 1 | 1 |
3 |
4 | 6 | 6 | 4 | 3 |
Wie man sieht, werden die Folgen zyklisch und es kommen in der oberen Zeile nur 1en und 5en vor. In der unteren Zeile gibt es keine 5en. Damit ist klar: Wenn es gemeinsame Folgenglieder gibt, sind diese also auf alle Fälle kongruent 1 modulo 5. Dafür kommen aber nur die Stellen 1,2 dann 9, 10 dann wieder 17,18 usw. in Frage. Wegen des schnellen Wachstums der Folge, kann man hiermit schon "ganz ordentliche Abschätzungen" bekommen. Diese lassen sich durch die geschickte Wahl des Moduls oder die Kombination mehrerer Module ganz erheblich in die Höhe treiben.
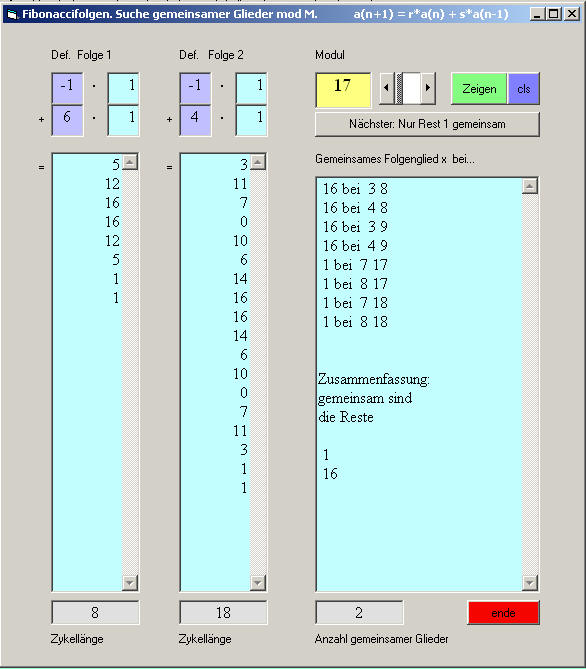
Das folgende Bild zeigt die Oberfläche eines Computerprogramms mit dessen Hilfe man beliebige rekursiv definierte Folgen zweiter Ordnung in einem frei wählbaren Modul untersuchen kann. Es kann zum Experimentieren heruntergeladen werden. Man kann mit diesem Programm beliebige rekursiv definierte Folgen des Typs an+1 = r ∙ an + s ∙ an-1 bezüglich eines frei wählbaren Moduls untersuchen. Betrachtet man "unsere Folgen" modulo 1459, so kann man zu einer "astronomischen Abschätzung" kommen:
Unter 10200 gibt es gewiß keine gemeinsamen Folgenglieder.
So sieht die Programmoberfläche aus:
Weiterarbeit
Man beweise die Unmöglichkeit möglichst in beiden Repräsentationen
Bei dem Versuch eine unendliche Folge von Modulen zu finden in denen nur die triviale viergliedrige arithmetische Progression aus quadratischen Resten existiert, fiel auf, daß alle diese Module Teiler von 3∙4∙5∙7∙11 = 4620 sind. Dies ist das Ergebnis einer systematischen Suche mit Hilfe eines Computers, es fehlt allerdings ein Beweis oder eine Widerlegung für eine entsprechende Vermutung für alle n. . Für eigene Erkundungen kann mit unserem Computerprogramm experimentiert werden (es ist "selbsterklärend").
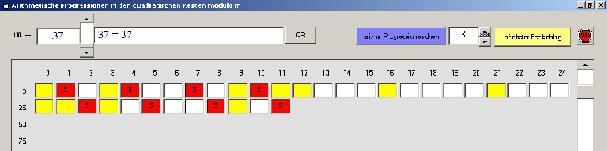
Bild: Im Modul M = 37 wurden zwei arithmetische Progressionen der Länge 4 mit der Differenz d=3 gefunden.
download des Programms
Zum Schluss: Ein Problem mit Lösungen
Drittelbare Sequenzen existieren nicht. Ist man weniger "streng" und erlaubt auch eine Einerlücke, oder Einerüberlappung, so findet man allerdings Beispiele, wie das folgende Bild zeigt (die Summe der natürlichen Zahlen in den dargestellten Abschnitten ist jeweils 495.